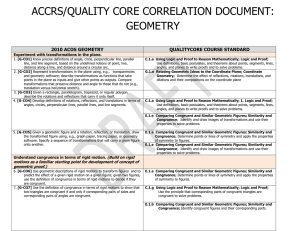
geometry pacing guide - Kalispell Public Schools
... Given a geometric figure and a rotation, reflection, or translation, draw the transformed figure using, e.g., graph paper, tracing paper, or geometry software. CC.9-12.G.CO.4 Develop definitions of rotations, reflections, and translations in terms of angles, ...
... Given a geometric figure and a rotation, reflection, or translation, draw the transformed figure using, e.g., graph paper, tracing paper, or geometry software. CC.9-12.G.CO.4 Develop definitions of rotations, reflections, and translations in terms of angles, ...
Geometry Scope and Sequence 2014
... B. Use coordinates to prove simple geometric theorems algebraically 4. Use coordinates to prove simple geometric theorems algebraically. For example, prove or disprove that a figure defined by four given points in the coordinate plane is a rectangle; prove or disprove that the point (1, √3) lies on ...
... B. Use coordinates to prove simple geometric theorems algebraically 4. Use coordinates to prove simple geometric theorems algebraically. For example, prove or disprove that a figure defined by four given points in the coordinate plane is a rectangle; prove or disprove that the point (1, √3) lies on ...
2.1-2.4 PowerPoint
... Inverse: If an animal is not a cat, then it does not have 4 paws. There are animals that are not cats that have 4 paws, so the inverse is false. Contrapositive: If an animal does not have 4 paws, then it is not a cat; True. Cats have 4 paws, so the contrapositive is true. Holt McDougal Geometry ...
... Inverse: If an animal is not a cat, then it does not have 4 paws. There are animals that are not cats that have 4 paws, so the inverse is false. Contrapositive: If an animal does not have 4 paws, then it is not a cat; True. Cats have 4 paws, so the contrapositive is true. Holt McDougal Geometry ...
Ohio Resource Center > Standards > Common Core > Mathematics
... transformations to decide if they are similar; explain using similarity transformations the meaning of similarity for triangles as the equality of all corresponding pairs of angles and the proportionality of all corresponding pairs of sides. HSG-SRT.A.3 Use the properties of similarity transformatio ...
... transformations to decide if they are similar; explain using similarity transformations the meaning of similarity for triangles as the equality of all corresponding pairs of angles and the proportionality of all corresponding pairs of sides. HSG-SRT.A.3 Use the properties of similarity transformatio ...
Properties of morphisms
... we still need infinitely many relations to describe B. Therefore, we say that f : A → B is of finite presentation if B ∼ = A[X1 , X2 , . . . , Xn ]/I for some integer n and some finitely generated ideal I. The property locally of finite presentation of morphisms of schemes is now easily defined (the noti ...
... we still need infinitely many relations to describe B. Therefore, we say that f : A → B is of finite presentation if B ∼ = A[X1 , X2 , . . . , Xn ]/I for some integer n and some finitely generated ideal I. The property locally of finite presentation of morphisms of schemes is now easily defined (the noti ...
cpctc - Cloudfront.net
... 4-6 Triangle Congruence: CPCTC Check It Out! Example 1 A landscape architect sets up the triangles shown in the figure to find the distance JK across a pond. What is JK? One angle pair is congruent, because they are vertical angles. ...
... 4-6 Triangle Congruence: CPCTC Check It Out! Example 1 A landscape architect sets up the triangles shown in the figure to find the distance JK across a pond. What is JK? One angle pair is congruent, because they are vertical angles. ...