Geometry 2: Remedial topology
... Definition 2.11. Let ∼ be an equivalence relation on a topological space M . Factor-topology (or quotient topology) is a topology on the set M/ ∼ of equivalence classes such that a subset U ⊂ M/ ∼ is open whenever its preimage in M is open. Exercise 2.17. Let G be a finite group acting on a Hausdorf ...
... Definition 2.11. Let ∼ be an equivalence relation on a topological space M . Factor-topology (or quotient topology) is a topology on the set M/ ∼ of equivalence classes such that a subset U ⊂ M/ ∼ is open whenever its preimage in M is open. Exercise 2.17. Let G be a finite group acting on a Hausdorf ...
Properties of Parallelograms
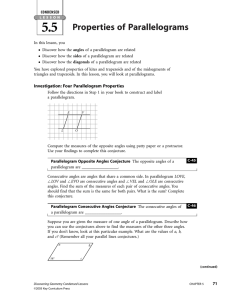
... Suppose you are given the measure of one angle of a parallelogram. Describe how you can use the conjectures above to find the measures of the other three angles. If you don’t know, look at this particular example. What are the values of a, b, and c? (Remember all your parallel lines conjectures.) a ...
... Suppose you are given the measure of one angle of a parallelogram. Describe how you can use the conjectures above to find the measures of the other three angles. If you don’t know, look at this particular example. What are the values of a, b, and c? (Remember all your parallel lines conjectures.) a ...
Scope Geo Reg FINAL - The School District of Palm Beach County
... MA.912.G.8.5 variety of ways to present deductive proofs, such as flow charts, paragraphs, two-column, and indirect proofs. ...
... MA.912.G.8.5 variety of ways to present deductive proofs, such as flow charts, paragraphs, two-column, and indirect proofs. ...