Slide 1 - ClassNet
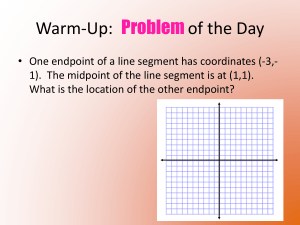
... Warm-Up: Problem of the Day • The points D(-3,2), E(4,-5), and F(6,2) form the vertices of a triangle. Show that the midsegment formed by the midpoints of EF and DF is half the length of DE and parallel to DE. ...
... Warm-Up: Problem of the Day • The points D(-3,2), E(4,-5), and F(6,2) form the vertices of a triangle. Show that the midsegment formed by the midpoints of EF and DF is half the length of DE and parallel to DE. ...
PDF
... † This text is available under the Creative Commons Attribution/Share-Alike License 3.0. You can reuse this document or portions thereof only if you do so under terms that are compatible with the CC-BY-SA license. ...
... † This text is available under the Creative Commons Attribution/Share-Alike License 3.0. You can reuse this document or portions thereof only if you do so under terms that are compatible with the CC-BY-SA license. ...
MISSOURI WESTERN STATE COLLEGE
... middle school teachers with the mathematical knowledge that they will need to teach mathematics in the elementary or middle school. STUDENT COMPETENCIES: In order to meet the above objective, successful students will: ...
... middle school teachers with the mathematical knowledge that they will need to teach mathematics in the elementary or middle school. STUDENT COMPETENCIES: In order to meet the above objective, successful students will: ...