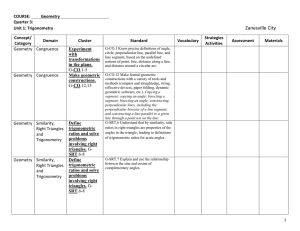
Geometry standards Unit 3
... 5. Prove the slope criteria for parallel and perpendicular lines and use them to solve geometric problems (e.g., find the equation of a line parallel or perpendicular to a given line that passes through a given point). 6. Find the point on a directed line segment between two given points that partit ...
... 5. Prove the slope criteria for parallel and perpendicular lines and use them to solve geometric problems (e.g., find the equation of a line parallel or perpendicular to a given line that passes through a given point). 6. Find the point on a directed line segment between two given points that partit ...
640109
... Title: Geometry and Measurement for Elementary Teaching Proposed Number: 01:640:109 Credits: 3 Effective: Fall 2011 Prerequisite: [Math 026 or Math 107 or placement into Math 111] and [Permission of Department] Co-req.: none Special Notation: Primarily for those intending to teach in grades K-8 Cour ...
... Title: Geometry and Measurement for Elementary Teaching Proposed Number: 01:640:109 Credits: 3 Effective: Fall 2011 Prerequisite: [Math 026 or Math 107 or placement into Math 111] and [Permission of Department] Co-req.: none Special Notation: Primarily for those intending to teach in grades K-8 Cour ...
Chapter 1
... can be verified. (See p. 72.) One can find a model for each of the 3 geometries; this shows that the parallel postulate is independent of the others. Euclidean: R2 . Elliptic: Crudely, “lines” are great circles on a sphere. They are not infinite, so we see there will be complications. Hyperbolic: a ...
... can be verified. (See p. 72.) One can find a model for each of the 3 geometries; this shows that the parallel postulate is independent of the others. Euclidean: R2 . Elliptic: Crudely, “lines” are great circles on a sphere. They are not infinite, so we see there will be complications. Hyperbolic: a ...
3/6 Quiz Review with reference sheet and answers File
... The length of each side of a triangle must be less than the sum of the lengths of the other two sides. Tips for classifying quadrilaterals: First check if it’s a parallelogram (both pairs opp. sides ≅, diagonals bisect each other, etc.). Then use converse of Pythagorean theorem to check for right an ...
... The length of each side of a triangle must be less than the sum of the lengths of the other two sides. Tips for classifying quadrilaterals: First check if it’s a parallelogram (both pairs opp. sides ≅, diagonals bisect each other, etc.). Then use converse of Pythagorean theorem to check for right an ...
k h b c b a q c p e a d r e m d f g n p r l m k g l q h n f
... Solution: Every compact connected surface is homeomorphic to S 2 , a connected sum of copies of P 2 , or a connected sum of copies of T 2 . Moreover, the surfaces in the above list are pairwise non-homeomorphic. The manifold above has 10 triangles, 15 edges, and 6 vertices. Its Euler characteristc i ...
... Solution: Every compact connected surface is homeomorphic to S 2 , a connected sum of copies of P 2 , or a connected sum of copies of T 2 . Moreover, the surfaces in the above list are pairwise non-homeomorphic. The manifold above has 10 triangles, 15 edges, and 6 vertices. Its Euler characteristc i ...
Geometry
... chart, guess-and-check, solving a simpler problem, writing an equation, and working backwards. ...
... chart, guess-and-check, solving a simpler problem, writing an equation, and working backwards. ...