class summary - Cornell Math
... 8. No single angle is greater than 180° 9. The triangle is contained in one-eighth of the sphere 10. The triangle is contained in an open hemisphere (one that does not contain the boundary) 11. Two sides do not contain antipodal points and the third side must be the shortest geodesic. Each of these ...
... 8. No single angle is greater than 180° 9. The triangle is contained in one-eighth of the sphere 10. The triangle is contained in an open hemisphere (one that does not contain the boundary) 11. Two sides do not contain antipodal points and the third side must be the shortest geodesic. Each of these ...
Triangle Similarity
... Use a flow chart, two-column proof, or paragraph proof to demonstrate the steps needed to prove that two triangles are similar Determine if two triangles are similar using triangle similarity conjectures (AA~, SAS~, SSS~) ...
... Use a flow chart, two-column proof, or paragraph proof to demonstrate the steps needed to prove that two triangles are similar Determine if two triangles are similar using triangle similarity conjectures (AA~, SAS~, SSS~) ...
Copyright © by Holt, Rinehart and Winston
... Dilations and Similarity in the Coordinate Plane You can prove that triangles in the coordinate plane are similar by using the Distance Formula to find the side lengths. Then apply SSS Similarity or SAS Similarity. Use the figure to prove that ABC ADE. Step 1 Determine a plan for proving the tr ...
... Dilations and Similarity in the Coordinate Plane You can prove that triangles in the coordinate plane are similar by using the Distance Formula to find the side lengths. Then apply SSS Similarity or SAS Similarity. Use the figure to prove that ABC ADE. Step 1 Determine a plan for proving the tr ...
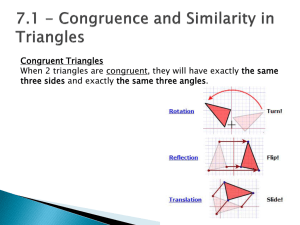
7.1 - Congruence and Similarity in Triangles
... Congruent Triangles When 2 triangles are congruent, they will have exactly the same three sides and exactly the same three angles. ...
... Congruent Triangles When 2 triangles are congruent, they will have exactly the same three sides and exactly the same three angles. ...
Prove Triangles are Congruent
... In a right triangle, the side opposite the right angle is called the hypotenuse. ...
... In a right triangle, the side opposite the right angle is called the hypotenuse. ...
4.2 Triangle Congruence by SSS and SAS
... 4.3 Triangle Congruence by ASA and AAS • You can prove that two triangles are congruent without having to show that all corresponding parts are congruent. – You will prove triangles congruent by using one pair of corresponding sides and two pairs of corresponding angles. ...
... 4.3 Triangle Congruence by ASA and AAS • You can prove that two triangles are congruent without having to show that all corresponding parts are congruent. – You will prove triangles congruent by using one pair of corresponding sides and two pairs of corresponding angles. ...
Geometry Chapter 4 Practice Test Name
... Write the converse of the following statement(s). Then tell whether the converse is True or False. 8. If a triangle has three congruent angles, then it is equilangular. ...
... Write the converse of the following statement(s). Then tell whether the converse is True or False. 8. If a triangle has three congruent angles, then it is equilangular. ...