Chapter 8A - Geometric Properties
... rectangle.” Who is right? Explain your answer on your graph paper. What is the fewest number of figures you would have to draw to display a square, a rhombus, a rectangle, a parallelogram, and a trapezoid? What are the figures? How are a square and a rectangle different? How are a parallelogram and ...
... rectangle.” Who is right? Explain your answer on your graph paper. What is the fewest number of figures you would have to draw to display a square, a rhombus, a rectangle, a parallelogram, and a trapezoid? What are the figures? How are a square and a rectangle different? How are a parallelogram and ...
Chapter 9A - Geometric Properties
... rectangle.” Who is right? Explain your answer on your graph paper. What is the fewest number of figures you would have to draw to display a square, a rhombus, a rectangle, a parallelogram, and a trapezoid? What are the figures? How are a square and a rectangle different? How are a parallelogram and ...
... rectangle.” Who is right? Explain your answer on your graph paper. What is the fewest number of figures you would have to draw to display a square, a rhombus, a rectangle, a parallelogram, and a trapezoid? What are the figures? How are a square and a rectangle different? How are a parallelogram and ...
Copyright © by Holt, Rinehart and Winston
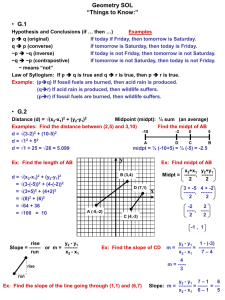
... 5. No, x x may not be 180. 6. slope of JK slope of LM 1; slope ...
... 5. No, x x may not be 180. 6. slope of JK slope of LM 1; slope ...
Practice 3A 1. What is the converse of the statement, “If a strawberry is
... 5. Which lines, if any, can you conclude are parallel given that m∠1+m∠2=180? Justify your conclusion with a theorem or postulate. A. j∥k, by the converse of the Same-‐Side Interior Angles Theorem B. ...
... 5. Which lines, if any, can you conclude are parallel given that m∠1+m∠2=180? Justify your conclusion with a theorem or postulate. A. j∥k, by the converse of the Same-‐Side Interior Angles Theorem B. ...