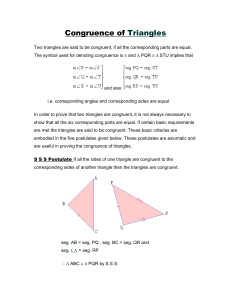
Congruence of Triangles
... H and G are two points on congruent sides DE & DF of DEF such that seg. DH seg. DG. Prove that seg. HF seg. GE. ...
... H and G are two points on congruent sides DE & DF of DEF such that seg. DH seg. DG. Prove that seg. HF seg. GE. ...
3. The parallel axiom Axiom 8 (Parallel Axiom). Given a line k, and a
... following formal definition. Two lines are not parallel if they have exactly one point in common; otherwise they are parallel. Theorem 3.1. In the set of all lines in the plane, the relation of being parallel is an equivalence relation. Proof. First, since a line has infinitely many points in common ...
... following formal definition. Two lines are not parallel if they have exactly one point in common; otherwise they are parallel. Theorem 3.1. In the set of all lines in the plane, the relation of being parallel is an equivalence relation. Proof. First, since a line has infinitely many points in common ...
Progression grid
... by completing the square and using the quadratic equation formula. (The quadratic equation formula is given on the formulae sheet. The technique of completing the square may also be used to write quadratic expressions in the form (x + a)2 + b and hence to find the minimum value of the expression and ...
... by completing the square and using the quadratic equation formula. (The quadratic equation formula is given on the formulae sheet. The technique of completing the square may also be used to write quadratic expressions in the form (x + a)2 + b and hence to find the minimum value of the expression and ...
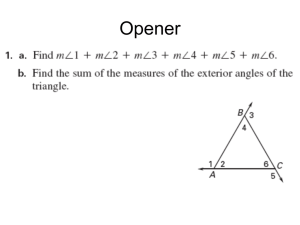
Justifying the Exterior Angle of a Triangle Theorem
... 1. The teacher asks the student to complete the problems on the Justifying the Exterior Angle of a Triangle Theorem worksheet. 2. The teacher asks follow-up questions, as needed. ...
... 1. The teacher asks the student to complete the problems on the Justifying the Exterior Angle of a Triangle Theorem worksheet. 2. The teacher asks follow-up questions, as needed. ...
Example 5 - Net Start Class
... You are given that two angles of ∆ABC are congruent to two angles of ∆DEF. By the Third Angles Theorem, the third angles are also congruent. That is, B E. Notice that BC is the side included between B and C, and EF is the side included between E and F. You can apply the ASA Congruence Postul ...
... You are given that two angles of ∆ABC are congruent to two angles of ∆DEF. By the Third Angles Theorem, the third angles are also congruent. That is, B E. Notice that BC is the side included between B and C, and EF is the side included between E and F. You can apply the ASA Congruence Postul ...