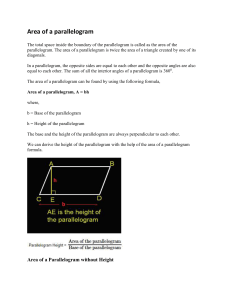
Area of a parallelogram
... Quadrilateral means a closed figure formed by four line segments and a parallelogram is a quadrilateral in which the opposite sides are parallel to each other. A point is used to represent a position in space. A ...
... Quadrilateral means a closed figure formed by four line segments and a parallelogram is a quadrilateral in which the opposite sides are parallel to each other. A point is used to represent a position in space. A ...
EUCLIDEAN, SPHERICAL AND HYPERBOLIC
... parallel rays (i.e., half-lines)1; each line thus has two (distinct) ends. We extend the hyperbolic plane H by adding a boundary ∂H consisting of all ends, which are called points at infinity (or infinite points or improper points); see Appendices A–C for concrete models. Each (proper) line thus has ...
... parallel rays (i.e., half-lines)1; each line thus has two (distinct) ends. We extend the hyperbolic plane H by adding a boundary ∂H consisting of all ends, which are called points at infinity (or infinite points or improper points); see Appendices A–C for concrete models. Each (proper) line thus has ...
Geo Module 1 - Federal Way Public Schools
... truth of our assumptions. For example, in Proposition 1, when Euclid said, “Let be the given finite straight line,” he assumed that, given any two distinct points there is exactly one line that contains them. Of course, that assumes we have two points! Best if we assume there are points in the plane ...
... truth of our assumptions. For example, in Proposition 1, when Euclid said, “Let be the given finite straight line,” he assumed that, given any two distinct points there is exactly one line that contains them. Of course, that assumes we have two points! Best if we assume there are points in the plane ...
Visualizing Hyperbolic Geometry
... A straight line segment can be extended indefinitely in a straight line. Given any straight line segment, a circle can be drawn having the segment as a radius and one endpoint as center. All right angles are congruent. If two lines are drawn which intersect a third in such a way that the sum of the ...
... A straight line segment can be extended indefinitely in a straight line. Given any straight line segment, a circle can be drawn having the segment as a radius and one endpoint as center. All right angles are congruent. If two lines are drawn which intersect a third in such a way that the sum of the ...
Selected Answers - Big Ideas Learning
... 33. deductive reasoning; Laws of nature and the Law of Syllogism were used to draw the conclusion. 35. The Law of Detachment cannot be used because the hypothesis is not true; Sample answer: Using the Law of Detachment, because a square is a rectangle, you can conclude that a square has four sides. ...
... 33. deductive reasoning; Laws of nature and the Law of Syllogism were used to draw the conclusion. 35. The Law of Detachment cannot be used because the hypothesis is not true; Sample answer: Using the Law of Detachment, because a square is a rectangle, you can conclude that a square has four sides. ...