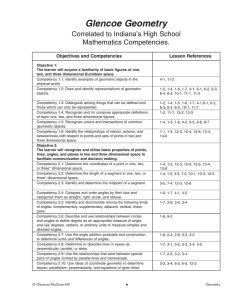
JMAP REGENTS BY COMMON CORE STATE STANDARD: TOPIC
... If chords FB and FC are drawn, which type of triangle, according to its angles, would FBC be? Explain your answer. ...
... If chords FB and FC are drawn, which type of triangle, according to its angles, would FBC be? Explain your answer. ...
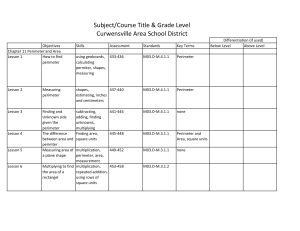
Grade 3 Math 3rd Quarter - Curwensville Area School District
... Chapter 11 Assessment Chapter 12 Two Dimensional Shapes Lesson 1 Describing Plane ...
... Chapter 11 Assessment Chapter 12 Two Dimensional Shapes Lesson 1 Describing Plane ...