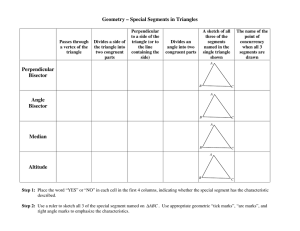
11.1 Angle Measures in Polygons
... number of sides in the polygon: triangle, quadrilateral, pentagon, hexagon, and so forth. The sum of the measures of the interior angles of a polygon also depends on the number of sides. ...
... number of sides in the polygon: triangle, quadrilateral, pentagon, hexagon, and so forth. The sum of the measures of the interior angles of a polygon also depends on the number of sides. ...
Day 4 – Similar Figures
... translations: a. Lines are taken to lines, and line segments to line segments of the same length. b. Angles are taken to angles of the same measure. c. Parallel lines are taken to parallel lines. • MCC8.G.2 Understand that a two‐dimensional figure is congruent to another if the second can be obtaine ...
... translations: a. Lines are taken to lines, and line segments to line segments of the same length. b. Angles are taken to angles of the same measure. c. Parallel lines are taken to parallel lines. • MCC8.G.2 Understand that a two‐dimensional figure is congruent to another if the second can be obtaine ...
Geometry Worksheet 1
... 15. If an angle measures x, write an expression to represent the measure of its supplement. _______________ 16. If an angle is twenty more than four times its supplement, find the measure of both angles. ...
... 15. If an angle measures x, write an expression to represent the measure of its supplement. _______________ 16. If an angle is twenty more than four times its supplement, find the measure of both angles. ...
Mathematics Explanations: Sections 2 and 4
... answered E, you may have mistakenly thought a cube had four faces. 14) E) To minimize the value of the fraction in the question, you must maximize the denominator, √ . √ will be largest when x itself is its largest, so E, the largest answer, is correct. By no means is it necessary to calculate th ...
... answered E, you may have mistakenly thought a cube had four faces. 14) E) To minimize the value of the fraction in the question, you must maximize the denominator, √ . √ will be largest when x itself is its largest, so E, the largest answer, is correct. By no means is it necessary to calculate th ...
Euclidean Parallel Postulate
... Euclidean Proposition 2.5. A line perpendicular to one of two parallel lines is perpendicular to the other. Euclidean Proposition 2.6. If l1, l2, l3, l4 are four distinct lines such that l1 is parallel to l2, l3 is perpendicular to l1, and l4 is perpendicular to l2, then l3 is parallel to l4. Euclid ...
... Euclidean Proposition 2.5. A line perpendicular to one of two parallel lines is perpendicular to the other. Euclidean Proposition 2.6. If l1, l2, l3, l4 are four distinct lines such that l1 is parallel to l2, l3 is perpendicular to l1, and l4 is perpendicular to l2, then l3 is parallel to l4. Euclid ...