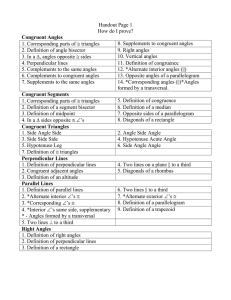
Complementary and Supplementary Notes
... 60° and 120° angles are complementary angles because 60° + 120° = 180°. Example: A 60° angle is called the supplement of the 120° angle. Similarly, the 120° angle is the supplement of the 60° angle. Practice: Find the supplement of each angle. b) 40° ...
... 60° and 120° angles are complementary angles because 60° + 120° = 180°. Example: A 60° angle is called the supplement of the 120° angle. Similarly, the 120° angle is the supplement of the 60° angle. Practice: Find the supplement of each angle. b) 40° ...
Discovery of Non-Euclidean Geometry
... AA , BB 0 , CC 0 , DD0 be segments perpendicular to l0 with feet A0 , B 0 , C 0 , D0 ∈ l0 . Note that ∠XP Q is acute, ∠CP Q is obtuse, and the angle sum of ¤P QC 0 C is less than 360◦ . Then ∠P CC 0 is acute. Of course ∠P CC 0 < ∠CP Q. So P Q < CC 0 by property of quadrilaterals with two base right ...
... AA , BB 0 , CC 0 , DD0 be segments perpendicular to l0 with feet A0 , B 0 , C 0 , D0 ∈ l0 . Note that ∠XP Q is acute, ∠CP Q is obtuse, and the angle sum of ¤P QC 0 C is less than 360◦ . Then ∠P CC 0 is acute. Of course ∠P CC 0 < ∠CP Q. So P Q < CC 0 by property of quadrilaterals with two base right ...
Glossary - Excel Math
... Adjoining Sides sides that meet to form the angles of a figure . . . . . . . . . . . . . . . [L14] 32 Alternate Exterior Angles outside angles on different parallel lines . . . . . . . [L88] 210 Alternate Interior Angles inside angles on different parallel lines . . . . . . . . . [L88] 210 AM (ante ...
... Adjoining Sides sides that meet to form the angles of a figure . . . . . . . . . . . . . . . [L14] 32 Alternate Exterior Angles outside angles on different parallel lines . . . . . . . [L88] 210 Alternate Interior Angles inside angles on different parallel lines . . . . . . . . . [L88] 210 AM (ante ...
Relationships Within a Circle
... The longest chord of a circle is a diameter. Any perpendicular bisector of a chord of a circle is a diameter. In a circle, any radius perpendicular to a chord divides that chord into two congruent segments. Theorem 4 In a circle, any radius perpendicular to a chord divides the subtended arc into two ...
... The longest chord of a circle is a diameter. Any perpendicular bisector of a chord of a circle is a diameter. In a circle, any radius perpendicular to a chord divides that chord into two congruent segments. Theorem 4 In a circle, any radius perpendicular to a chord divides the subtended arc into two ...