Download 6-2: Proving Congruence using congruent parts

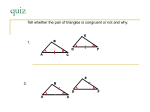
6-2: Proving Congruence
using congruent parts
Unit 6
English Casbarro
Congruent Figures
 Naming figures must be done
correctly, so that you can write
accurate congruence statements.
If you are trying to determine if two triangles are congruent,
you will compare the angles and the sides. If all pairs of angles
are congruent and all pairs of sides are congruent,
then the triangles are congruent to each other.
Postulate shortcuts to Proving
Congruence of Triangles
 SSSif the three sides of one triangle
are congruent to the three sides of
another triangle, the triangles are
congruent.
 SASif two sides and the included
angle of one triangle are congruent to
two sides and the included angle of
another triangle, then the triangles
are congruent
Postulate shortcuts to Proving
Congruence of Triangles
 ASAif two angles and the included side
of one triangle are congruent to two
angles and the included side of another
triangle the triangles are congruent.
 AASif two angles and a non-included
side of one triangle are congruent to two
angles and a non-included side of
another triangle, then the triangles are
congruent.
CPCTC: Corresponding parts of
Congruent Triangles are Congruent
Turn in the following problems
1.
2.