Maths E3 GCSE - Churchill Park School
... Support: I can measure, compare, add and subtract length (S13) Core: I know angles are measured in degrees; I can estimate and measure them and draw a given angle, writing its size in degrees (S15) Extension: I can use Pythagoras’ Theorem to solve problems involving right-angled triangles (S19, GCSE ...
... Support: I can measure, compare, add and subtract length (S13) Core: I know angles are measured in degrees; I can estimate and measure them and draw a given angle, writing its size in degrees (S15) Extension: I can use Pythagoras’ Theorem to solve problems involving right-angled triangles (S19, GCSE ...
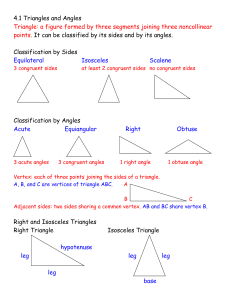
Lap 6 Definitions and Conjectures Congruent Circles: Two or more
... Congruent Circles: Two or more circles with congruent radii. Concentric Circles: Two or more circles sharing the same center. Radius: A segment with one endpoint the center of the circle and the other one on the circle. Chord: A segment with endpoints on the circle (The diameter IS a chord). Diamete ...
... Congruent Circles: Two or more circles with congruent radii. Concentric Circles: Two or more circles sharing the same center. Radius: A segment with one endpoint the center of the circle and the other one on the circle. Chord: A segment with endpoints on the circle (The diameter IS a chord). Diamete ...