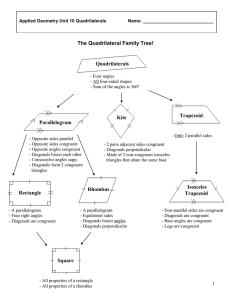
Chapter 3-Parallel and Perpendicular Lines
... 55. Write a paragraph proof of this theorem: In a plane, if two lines are perpendicular to the same line, then they are parallel to each other. Given: Prove: ...
... 55. Write a paragraph proof of this theorem: In a plane, if two lines are perpendicular to the same line, then they are parallel to each other. Given: Prove: ...
Discrepancies Between Euclidean and Spherical Trigonometry
... law of cosines and law of sines in Euclidean trigonometry. The first step is to derive a trigonometry for right triangles. The measure of the angle formed by the intersection of two great circles is defined to be equal to the measure of the angle formed by the two lines tangent to each great circle ...
... law of cosines and law of sines in Euclidean trigonometry. The first step is to derive a trigonometry for right triangles. The measure of the angle formed by the intersection of two great circles is defined to be equal to the measure of the angle formed by the two lines tangent to each great circle ...
Morley`s Miracle - Teachers of India
... 1. In triangles ARB, BPC, CQA, we know the bases - AB, BC, and AC and the adjacent angles. TheLaw of Sines then yields the segments AR, BR, BP, CP, CQ, and AQ. 2. Next we apply the Law of Cosines to triangles AQR, BPR, and CPQ to determine (and compare) the segments QR, PR, and PQ. The fact that th ...
... 1. In triangles ARB, BPC, CQA, we know the bases - AB, BC, and AC and the adjacent angles. TheLaw of Sines then yields the segments AR, BR, BP, CP, CQ, and AQ. 2. Next we apply the Law of Cosines to triangles AQR, BPR, and CPQ to determine (and compare) the segments QR, PR, and PQ. The fact that th ...
Illinois ABE/ASE Mathematics Content Standards
... mathematics standards must also respect what is known about how students learn. As Confrey (2007) points out, developing “sequenced obstacles and challenges for students…absent the insights about meaning that derive from careful study of learning, would be unfortunate and unwise.” In recognition of ...
... mathematics standards must also respect what is known about how students learn. As Confrey (2007) points out, developing “sequenced obstacles and challenges for students…absent the insights about meaning that derive from careful study of learning, would be unfortunate and unwise.” In recognition of ...