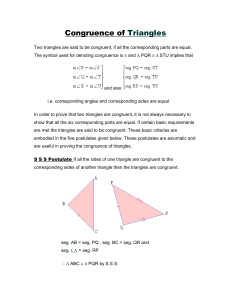
Periodic Billiard Paths in Triangles
... Let a point move on a frictionless plane bounded by a triangle If it hits a corner (a vertex), then it stops If it hits a side (an edge), then it changes its direction such that the angle of reflection is equal to the angle of incidence The path that the point follows is called a billiard path An in ...
... Let a point move on a frictionless plane bounded by a triangle If it hits a corner (a vertex), then it stops If it hits a side (an edge), then it changes its direction such that the angle of reflection is equal to the angle of incidence The path that the point follows is called a billiard path An in ...
Document
... SSS, SAS, ASA, or AAS. If it is not possible to prove that they are congruent, write not possible. Ex 4 ...
... SSS, SAS, ASA, or AAS. If it is not possible to prove that they are congruent, write not possible. Ex 4 ...
6.1 Polygons - Teacher Notes
... 6, 7, and 8 sides • Divide Each Polygon into triangles by drawing all diagonals that are possible from one vertex • Multiply the number of triangles by 180 to find the sum of the measures of the angles of each polygon. ...
... 6, 7, and 8 sides • Divide Each Polygon into triangles by drawing all diagonals that are possible from one vertex • Multiply the number of triangles by 180 to find the sum of the measures of the angles of each polygon. ...
GETE0305
... This number is not an integer. 39. Critical Thinking A triangle has two congruent angles and an exterior angle with measure 100. Find two possible sets of measures for the angles of the triangle. ...
... This number is not an integer. 39. Critical Thinking A triangle has two congruent angles and an exterior angle with measure 100. Find two possible sets of measures for the angles of the triangle. ...