Unit 2 - Long Beach Unified School District
... Understand that a two-dimensional figure is congruent to another if the second can be obtained from the first by a sequence of rotations, reflections, and translations; given two congruent figures, describe a sequence that exhibits the congruence between them. Describe the effect of dilations, trans ...
... Understand that a two-dimensional figure is congruent to another if the second can be obtained from the first by a sequence of rotations, reflections, and translations; given two congruent figures, describe a sequence that exhibits the congruence between them. Describe the effect of dilations, trans ...
Learning Target - Mattawan Consolidated School
... Geometry Chapter 4 Lesson 6: Triangle Congruence: CPCTC Learning Target: Use corresponding parts of congruent triangles to prove statements about triangles and/or solve problems involving triangles. You can use congruent triangles to estimate distances. Ex1: A and B are on the edges of a ravine. Wh ...
... Geometry Chapter 4 Lesson 6: Triangle Congruence: CPCTC Learning Target: Use corresponding parts of congruent triangles to prove statements about triangles and/or solve problems involving triangles. You can use congruent triangles to estimate distances. Ex1: A and B are on the edges of a ravine. Wh ...
Answers to questions students asked about the study guide
... Common notions do are about `equality’ not about the particular subject matter. These include properties of equalities and congruence: e.g. transitivity of equality or congruence and “equals added to equals are equal”. Postulates are properties of geometry: any two lines have a unique intersection o ...
... Common notions do are about `equality’ not about the particular subject matter. These include properties of equalities and congruence: e.g. transitivity of equality or congruence and “equals added to equals are equal”. Postulates are properties of geometry: any two lines have a unique intersection o ...
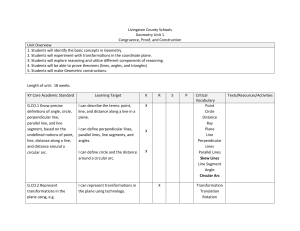
Livingston County Schools Geometry Unit 1 Congruence, Proof, and
... Geometry Unit 1 Congruence, Proof, and Construction Unit Overview 1. Students will identify the basic concepts in Geometry. 2. Students will experiment with transformations in the coordinate plane. 3. Students will explore reasoning and utilize different components of reasoning. 4. Students will be ...
... Geometry Unit 1 Congruence, Proof, and Construction Unit Overview 1. Students will identify the basic concepts in Geometry. 2. Students will experiment with transformations in the coordinate plane. 3. Students will explore reasoning and utilize different components of reasoning. 4. Students will be ...
File - Sine of Madness
... If one side of a triangle is longer than another side, then the angle opposite the longer side is larger than the angle opposite the shorter side and vice-versa. **Remember** Biggest angle is opposite the longest side and the smallest angle is opposite the shortest side. Make sure that you read what ...
... If one side of a triangle is longer than another side, then the angle opposite the longer side is larger than the angle opposite the shorter side and vice-versa. **Remember** Biggest angle is opposite the longest side and the smallest angle is opposite the shortest side. Make sure that you read what ...
History of geometry

Geometry (from the Ancient Greek: γεωμετρία; geo- ""earth"", -metron ""measurement"") arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers (arithmetic).Classic geometry was focused in compass and straightedge constructions. Geometry was revolutionized by Euclid, who introduced mathematical rigor and the axiomatic method still in use today. His book, The Elements is widely considered the most influential textbook of all time, and was known to all educated people in the West until the middle of the 20th century.In modern times, geometric concepts have been generalized to a high level of abstraction and complexity, and have been subjected to the methods of calculus and abstract algebra, so that many modern branches of the field are barely recognizable as the descendants of early geometry. (See Areas of mathematics and Algebraic geometry.)