tasks - Georgia Mathematics Educator Forum
... Interpret units in the context of the problem. Convert units and rates using dimensional analysis (English–to–English and Metric–to– Metric without conversion factor provided and between English and Metric with conversion factor); Identify the different parts of the expression or formula and e ...
... Interpret units in the context of the problem. Convert units and rates using dimensional analysis (English–to–English and Metric–to– Metric without conversion factor provided and between English and Metric with conversion factor); Identify the different parts of the expression or formula and e ...
Study Guide - Quadrilaterals
... a. Q: Are the diagonals congruent? (Do not assume the diagonals are perpendicular to each other nor that they bisect one another.) b. Q2: Are the diagonals perpendicular to each other? c. Q3: Are the diagonals bisecting each other? d. Q4: Is there another property of diagonals worth mentioning? e. J ...
... a. Q: Are the diagonals congruent? (Do not assume the diagonals are perpendicular to each other nor that they bisect one another.) b. Q2: Are the diagonals perpendicular to each other? c. Q3: Are the diagonals bisecting each other? d. Q4: Is there another property of diagonals worth mentioning? e. J ...
pythagorean theorem - washingtonsegmented
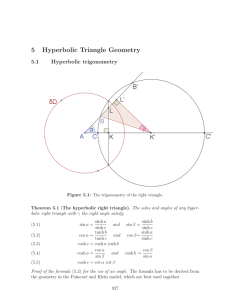
... The two triangles are similar because both triangles have a right angle and the two lines that cross form vertical angles (meaning they are equal in measure) and the remaining angles are congruent because triangles have 180º. Similarity establishes that corresponding sides are in a fixed ratio. Pyth ...
... The two triangles are similar because both triangles have a right angle and the two lines that cross form vertical angles (meaning they are equal in measure) and the remaining angles are congruent because triangles have 180º. Similarity establishes that corresponding sides are in a fixed ratio. Pyth ...
Congruence Criteria for Triangles—SAA and HL
... Based on your observations, why can’t we categorize AAA as congruence criterion? Is there any situation in which AAA does guarantee congruence? Even though the angle measures may be the same, the sides can be proportionally larger; you can have similar triangles in addition to a congruent triangle. ...
... Based on your observations, why can’t we categorize AAA as congruence criterion? Is there any situation in which AAA does guarantee congruence? Even though the angle measures may be the same, the sides can be proportionally larger; you can have similar triangles in addition to a congruent triangle. ...
History of geometry

Geometry (from the Ancient Greek: γεωμετρία; geo- ""earth"", -metron ""measurement"") arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers (arithmetic).Classic geometry was focused in compass and straightedge constructions. Geometry was revolutionized by Euclid, who introduced mathematical rigor and the axiomatic method still in use today. His book, The Elements is widely considered the most influential textbook of all time, and was known to all educated people in the West until the middle of the 20th century.In modern times, geometric concepts have been generalized to a high level of abstraction and complexity, and have been subjected to the methods of calculus and abstract algebra, so that many modern branches of the field are barely recognizable as the descendants of early geometry. (See Areas of mathematics and Algebraic geometry.)