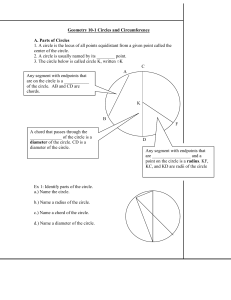
Geometry 10-1 Circles and Circumference
... 1. The circumference is the distance around a circle. 2. The circumference around a circle is often represented by the letter C. 3. The ratio between the circumference of a circle and it’s diameter is about 3:1. For each diameter, circumference is a little more than 3. 4. For a circumference of C un ...
... 1. The circumference is the distance around a circle. 2. The circumference around a circle is often represented by the letter C. 3. The ratio between the circumference of a circle and it’s diameter is about 3:1. For each diameter, circumference is a little more than 3. 4. For a circumference of C un ...
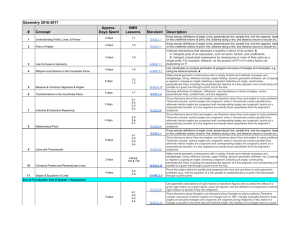
Geometry 2016-2017 # Concept Approx. Days Spent HMH Lessons
... Use coordinates to prove simple geometric theorems algebraically. For example, prove or disprove that a figure defined by four given points in the coordinate plane is a rectangle; prove or disprove that the point (1, √3) lies on the circle centered at the origin and containing the point (0, ...
... Use coordinates to prove simple geometric theorems algebraically. For example, prove or disprove that a figure defined by four given points in the coordinate plane is a rectangle; prove or disprove that the point (1, √3) lies on the circle centered at the origin and containing the point (0, ...
6.6 Special Quadrilaterals
... be the midpoints of the sides of any quadrilateral, ABCD E as shown. D If you draw AC, the Midsegment Theorem for H triangles says that FG║AC and EG║AC, so FG║EH. C Similar reasoning shows that EF║HG. So by definition, EFGH is a parallelogram. ...
... be the midpoints of the sides of any quadrilateral, ABCD E as shown. D If you draw AC, the Midsegment Theorem for H triangles says that FG║AC and EG║AC, so FG║EH. C Similar reasoning shows that EF║HG. So by definition, EFGH is a parallelogram. ...
History of geometry

Geometry (from the Ancient Greek: γεωμετρία; geo- ""earth"", -metron ""measurement"") arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers (arithmetic).Classic geometry was focused in compass and straightedge constructions. Geometry was revolutionized by Euclid, who introduced mathematical rigor and the axiomatic method still in use today. His book, The Elements is widely considered the most influential textbook of all time, and was known to all educated people in the West until the middle of the 20th century.In modern times, geometric concepts have been generalized to a high level of abstraction and complexity, and have been subjected to the methods of calculus and abstract algebra, so that many modern branches of the field are barely recognizable as the descendants of early geometry. (See Areas of mathematics and Algebraic geometry.)