Provided AC is a diameter, angle at B
... • This method was then applied to other practical purposes the navegation. Is further assumed that Thales already knew many of the foundations of geometry, such as the fact that any diameter of a circle is divided into identical parts, that an isosceles triangle has by force two equal angles at its ...
... • This method was then applied to other practical purposes the navegation. Is further assumed that Thales already knew many of the foundations of geometry, such as the fact that any diameter of a circle is divided into identical parts, that an isosceles triangle has by force two equal angles at its ...
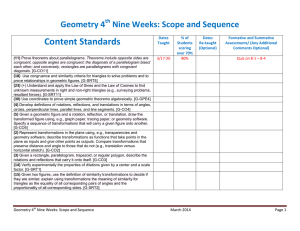
Geometry 4th Nine Weeks Scope and
... line segment based on the undefined notions of point, line, distance along a line, and distance around a circular arc. [G-CO1] (26) Construct the inscribed and circumscribed circles of a triangle, and prove properties of angles for a quadrilateral inscribed in a circle. [G-C3] (28) Derive, using sim ...
... line segment based on the undefined notions of point, line, distance along a line, and distance around a circular arc. [G-CO1] (26) Construct the inscribed and circumscribed circles of a triangle, and prove properties of angles for a quadrilateral inscribed in a circle. [G-C3] (28) Derive, using sim ...
Geometer Sketchpad - Stanford University
... lengths of the sides that include the angle and adjacent angles change. Why? What property have you discover about the quadrilateral inscribe in a circle. Can you prove that it is correct? Questions (mostly adapted from SimCalc’s discussion questions prepared by Gloria, Johnnie and Jennifer) What ...
... lengths of the sides that include the angle and adjacent angles change. Why? What property have you discover about the quadrilateral inscribe in a circle. Can you prove that it is correct? Questions (mostly adapted from SimCalc’s discussion questions prepared by Gloria, Johnnie and Jennifer) What ...
History of geometry

Geometry (from the Ancient Greek: γεωμετρία; geo- ""earth"", -metron ""measurement"") arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers (arithmetic).Classic geometry was focused in compass and straightedge constructions. Geometry was revolutionized by Euclid, who introduced mathematical rigor and the axiomatic method still in use today. His book, The Elements is widely considered the most influential textbook of all time, and was known to all educated people in the West until the middle of the 20th century.In modern times, geometric concepts have been generalized to a high level of abstraction and complexity, and have been subjected to the methods of calculus and abstract algebra, so that many modern branches of the field are barely recognizable as the descendants of early geometry. (See Areas of mathematics and Algebraic geometry.)