6-12 Comp 3 trainer notes - Math6-12TestPrep
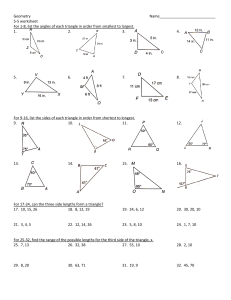
... 13. Apply the theorems pertaining to the relationships of chords, secants, diameters, radii, and tangents with respect to circles and to each other. 14. Apply the theorems pertaining to the measures of inscribed angles and angles formed by chords, secants, and tangents. 15. Identify basic geometric ...
... 13. Apply the theorems pertaining to the relationships of chords, secants, diameters, radii, and tangents with respect to circles and to each other. 14. Apply the theorems pertaining to the measures of inscribed angles and angles formed by chords, secants, and tangents. 15. Identify basic geometric ...
02 Spherical Geometry Basics
... other point is not the south pole, the shortest distance along the sphere is obvsiouly to go due south. We are, from now on, going to rule out pairs of antipodal points such as the north and south poles, because there are infinitely many geodesics between them. Otherwise, just as in geometry for the ...
... other point is not the south pole, the shortest distance along the sphere is obvsiouly to go due south. We are, from now on, going to rule out pairs of antipodal points such as the north and south poles, because there are infinitely many geodesics between them. Otherwise, just as in geometry for the ...
History of geometry

Geometry (from the Ancient Greek: γεωμετρία; geo- ""earth"", -metron ""measurement"") arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers (arithmetic).Classic geometry was focused in compass and straightedge constructions. Geometry was revolutionized by Euclid, who introduced mathematical rigor and the axiomatic method still in use today. His book, The Elements is widely considered the most influential textbook of all time, and was known to all educated people in the West until the middle of the 20th century.In modern times, geometric concepts have been generalized to a high level of abstraction and complexity, and have been subjected to the methods of calculus and abstract algebra, so that many modern branches of the field are barely recognizable as the descendants of early geometry. (See Areas of mathematics and Algebraic geometry.)