Second Semester Topics
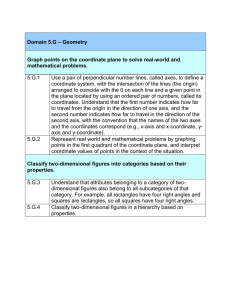
... Given a statement, be able to determine if it is true in Euclidean Geometry and/or Taxicab Geometry Given a statement, be able to determine if it is true in plane Geometry and/or spherical Geometry ...
... Given a statement, be able to determine if it is true in Euclidean Geometry and/or Taxicab Geometry Given a statement, be able to determine if it is true in plane Geometry and/or spherical Geometry ...
Proving Quadrilaterals Scaffolded WS
... show these types of lines? 13. Plot and label the figure. Name all four sides. 14. Show with mathematical calculations that adjacent sides make right angles to prove EFGH is a rectangle. ...
... show these types of lines? 13. Plot and label the figure. Name all four sides. 14. Show with mathematical calculations that adjacent sides make right angles to prove EFGH is a rectangle. ...
Document
... 13. _____ An angle can be named by its vertex. 14. _____ A line contains two planes. 15. _____ If A, B, and C are distinct point on a line, then AB + BC = AC. 16. _____ A midpoint must be positive. 17. _____ If line k lies in plane M, then the intersection of the line k and plane M is a point. Alway ...
... 13. _____ An angle can be named by its vertex. 14. _____ A line contains two planes. 15. _____ If A, B, and C are distinct point on a line, then AB + BC = AC. 16. _____ A midpoint must be positive. 17. _____ If line k lies in plane M, then the intersection of the line k and plane M is a point. Alway ...
ahsge - Walker County Schools
... Apply the Pythagorean Theorem and its converse to solve application problems, including expressing answers in simplified radical form or as decimal approximations and using Pythagorean triples where applicable Proving the Pythagorean Theorem ...
... Apply the Pythagorean Theorem and its converse to solve application problems, including expressing answers in simplified radical form or as decimal approximations and using Pythagorean triples where applicable Proving the Pythagorean Theorem ...
Study Portfolio
... You must write the title of the unit and its number. All future study sheets will need to have the same sections! Section #1: Vocabulary (words and/or diagrams) Angle of elevation (include a diagram) Angle of depression (include a diagram) SOH - CAH – TOA Co-function Section #2: Formulas/Equ ...
... You must write the title of the unit and its number. All future study sheets will need to have the same sections! Section #1: Vocabulary (words and/or diagrams) Angle of elevation (include a diagram) Angle of depression (include a diagram) SOH - CAH – TOA Co-function Section #2: Formulas/Equ ...
Tools for Proofs
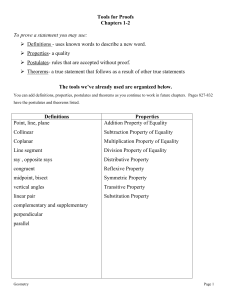
... Tools for Proofs Chapters 1-2 To prove a statement you may use: Definitions - uses known words to describe a new word. Properties- a quality Postulates- rules that are accepted without proof. Theorems- a true statement that follows as a result of other true statements The tools we’ve already ...
... Tools for Proofs Chapters 1-2 To prove a statement you may use: Definitions - uses known words to describe a new word. Properties- a quality Postulates- rules that are accepted without proof. Theorems- a true statement that follows as a result of other true statements The tools we’ve already ...
History of geometry

Geometry (from the Ancient Greek: γεωμετρία; geo- ""earth"", -metron ""measurement"") arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers (arithmetic).Classic geometry was focused in compass and straightedge constructions. Geometry was revolutionized by Euclid, who introduced mathematical rigor and the axiomatic method still in use today. His book, The Elements is widely considered the most influential textbook of all time, and was known to all educated people in the West until the middle of the 20th century.In modern times, geometric concepts have been generalized to a high level of abstraction and complexity, and have been subjected to the methods of calculus and abstract algebra, so that many modern branches of the field are barely recognizable as the descendants of early geometry. (See Areas of mathematics and Algebraic geometry.)