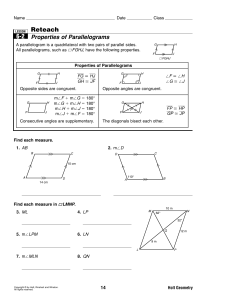
6-2 Reteach Properties of Parallelograms
... is c, so its area is _12_ bc. The areas of congruent triangles are equal, so the area of 䉭CGF is also _12_ bc. The height of 䉭DGH is b and the length of the base is c, so its area is _12_ bc. The area of 䉭BEF is also _12_ bc. The area of all four triangles is thus 2bc. The area of EFGH is the area o ...
... is c, so its area is _12_ bc. The areas of congruent triangles are equal, so the area of 䉭CGF is also _12_ bc. The height of 䉭DGH is b and the length of the base is c, so its area is _12_ bc. The area of 䉭BEF is also _12_ bc. The area of all four triangles is thus 2bc. The area of EFGH is the area o ...
4-4 Notes
... GEOMETRY SECTION 4.4 NOTES – PROVING TRIANGLES CONGRUENT (ASA and AAS) Learning Targets: -Prove two triangles congruent using ASA - Prove two triangles congruent using AAS ***Proof Hints*** ...
... GEOMETRY SECTION 4.4 NOTES – PROVING TRIANGLES CONGRUENT (ASA and AAS) Learning Targets: -Prove two triangles congruent using ASA - Prove two triangles congruent using AAS ***Proof Hints*** ...
Fourth Grade Mathematics Newsletter MT Learning Goals by Measurement Topic (MT)
... generate multiple ways to find solutions to word problems. make adjustments to thinking when problem solving. recognize that… o mistakes can help one learn. o skillful students ask for help and feedback. o it is okay to not understand everything the first time around. o everyone is capable of high a ...
... generate multiple ways to find solutions to word problems. make adjustments to thinking when problem solving. recognize that… o mistakes can help one learn. o skillful students ask for help and feedback. o it is okay to not understand everything the first time around. o everyone is capable of high a ...
Chapter 7 Geometry
... justifying informally by paper folding or cutting, and testing by measuring, that the interior angle sum of a triangle is 180, and that any exterior angle equals the sum of the two interior opposite angles applying geometrical facts, properties and relationships to solve numerical problems such ...
... justifying informally by paper folding or cutting, and testing by measuring, that the interior angle sum of a triangle is 180, and that any exterior angle equals the sum of the two interior opposite angles applying geometrical facts, properties and relationships to solve numerical problems such ...
What`s a Widget_NOTES.notebook
... see, Geometry is like taking a foreign language class. I need you to be able to understand what I speak, and I need you to be able to speak it back to me. So...we are going to build our vocabulary today. No worries...this will all be review for you. ...
... see, Geometry is like taking a foreign language class. I need you to be able to understand what I speak, and I need you to be able to speak it back to me. So...we are going to build our vocabulary today. No worries...this will all be review for you. ...
History of geometry

Geometry (from the Ancient Greek: γεωμετρία; geo- ""earth"", -metron ""measurement"") arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers (arithmetic).Classic geometry was focused in compass and straightedge constructions. Geometry was revolutionized by Euclid, who introduced mathematical rigor and the axiomatic method still in use today. His book, The Elements is widely considered the most influential textbook of all time, and was known to all educated people in the West until the middle of the 20th century.In modern times, geometric concepts have been generalized to a high level of abstraction and complexity, and have been subjected to the methods of calculus and abstract algebra, so that many modern branches of the field are barely recognizable as the descendants of early geometry. (See Areas of mathematics and Algebraic geometry.)























