Task - Illustrative Mathematics
... this subject comes up, the teacher may wish to make explicit that the picture may be used as justification of this fact. Providing a more rigorous mathematical explanation goes beyond the scope of the high school standards. A second solution is provided emphasizing rigid motions. The argument has tw ...
... this subject comes up, the teacher may wish to make explicit that the picture may be used as justification of this fact. Providing a more rigorous mathematical explanation goes beyond the scope of the high school standards. A second solution is provided emphasizing rigid motions. The argument has tw ...
Activity 6-6
... What do you notice about all of the acute angles? ________________________________________ Therefore, all of the acute angles on the left side of the figure are ______________________ to each other. What do you notice about all of the obtuse angles? _______________________________________ Therefore, ...
... What do you notice about all of the acute angles? ________________________________________ Therefore, all of the acute angles on the left side of the figure are ______________________ to each other. What do you notice about all of the obtuse angles? _______________________________________ Therefore, ...
Isosceles Triangle Investigation Name(s): DIRECTIONS: Use any
... 2) Use the “Properties of Isosceles Triangles” worksheet to construct an isosceles triangle using Geometer’s Sketchpad. Cut and paste your triangle below (shrink it so it doesn’t take up too much space after you paste it below) ...
... 2) Use the “Properties of Isosceles Triangles” worksheet to construct an isosceles triangle using Geometer’s Sketchpad. Cut and paste your triangle below (shrink it so it doesn’t take up too much space after you paste it below) ...
8-4 powerpoint/notes - Nutley Public Schools
... and let B represent the top of the Space Needle. Let y be the height of the Space Needle. Holt McDougal Geometry ...
... and let B represent the top of the Space Needle. Let y be the height of the Space Needle. Holt McDougal Geometry ...
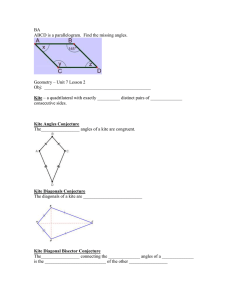
Unit 7 Lesson 2 - Trimble County Schools
... Midsegment – the segment connecting the _________________ of two nonparallel sides of a _____________ ______ ____________________ Three Midsegments Conjecture The three ________________ of a triangle divide it into __________ congruent triangles. ...
... Midsegment – the segment connecting the _________________ of two nonparallel sides of a _____________ ______ ____________________ Three Midsegments Conjecture The three ________________ of a triangle divide it into __________ congruent triangles. ...
1.2
... The second undefined geometric term is line. A line is an infinite set of points. Given any two points on a line, there is always a point that lies between them on that line. Lines have a quality of “straightness” that is not defined but assumed. Given several points on a line, these points form a s ...
... The second undefined geometric term is line. A line is an infinite set of points. Given any two points on a line, there is always a point that lies between them on that line. Lines have a quality of “straightness” that is not defined but assumed. Given several points on a line, these points form a s ...
Euclidean geometry

Euclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions (theorems) from these. Although many of Euclid's results had been stated by earlier mathematicians, Euclid was the first to show how these propositions could fit into a comprehensive deductive and logical system. The Elements begins with plane geometry, still taught in secondary school as the first axiomatic system and the first examples of formal proof. It goes on to the solid geometry of three dimensions. Much of the Elements states results of what are now called algebra and number theory, explained in geometrical language.For more than two thousand years, the adjective ""Euclidean"" was unnecessary because no other sort of geometry had been conceived. Euclid's axioms seemed so intuitively obvious (with the possible exception of the parallel postulate) that any theorem proved from them was deemed true in an absolute, often metaphysical, sense. Today, however, many other self-consistent non-Euclidean geometries are known, the first ones having been discovered in the early 19th century. An implication of Albert Einstein's theory of general relativity is that physical space itself is not Euclidean, and Euclidean space is a good approximation for it only where the gravitational field is weak.Euclidean geometry is an example of synthetic geometry, in that it proceeds logically from axioms to propositions without the use of coordinates. This is in contrast to analytic geometry, which uses coordinates.