Normed vector spaces
... Examples 3.11. The following are Hilbert spaces, when equipped with their usual inner products: Fn ; `2 (S), where S is a set; and L2 (M ), where M is a measure space. We showed that `p (S) is complete in Topic 2; in particular, `2 (S) is complete. The case of L2 (M ) is similar, but requires integr ...
... Examples 3.11. The following are Hilbert spaces, when equipped with their usual inner products: Fn ; `2 (S), where S is a set; and L2 (M ), where M is a measure space. We showed that `p (S) is complete in Topic 2; in particular, `2 (S) is complete. The case of L2 (M ) is similar, but requires integr ...
![MATH 409, Fall 2013 [3mm] Advanced Calculus I](http://s1.studyres.com/store/data/019184906_1-2ea198de2d20e978c4b1d91fadeb6dab-300x300.png)
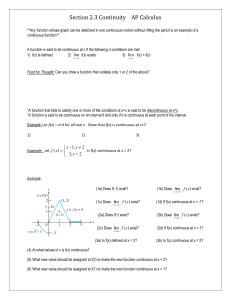
Section 2.3 Continuity AP Calculus - AP Calculus
... Theorem: If f(x) is continuous on a closed interval [a, b] and f(a) f(b), then for every value M between f(a) and f(b), there exists at least one value c (a, b) such that f(c) = M. *Corollary: If f(x) is continuous on [a, b] and if f(a) and f(b) are nonzero and have opposite signs, then f(x) has ...
... Theorem: If f(x) is continuous on a closed interval [a, b] and f(a) f(b), then for every value M between f(a) and f(b), there exists at least one value c (a, b) such that f(c) = M. *Corollary: If f(x) is continuous on [a, b] and if f(a) and f(b) are nonzero and have opposite signs, then f(x) has ...
Week 3. Functions: Piecewise, Even and Odd.
... numbers x ∈ R such that f(x) makes sense.) • What is the range of f? (The range of f is the set of all numbers ...
... numbers x ∈ R such that f(x) makes sense.) • What is the range of f? (The range of f is the set of all numbers ...
Defining Functions
... x:xs patterns must be parenthesised, because application has priority over (:). For example, the following definition gives an error: head x:_ = x ...
... x:xs patterns must be parenthesised, because application has priority over (:). For example, the following definition gives an error: head x:_ = x ...
Slide 1
... A function P is called a polynomial if P(x) = anxn + an-1xn-1 + … + a2x2 + a1x + a0 where n is a nonnegative integer and the numbers a0, a1, a2, …, an are constants called the coefficients of the polynomial. ...
... A function P is called a polynomial if P(x) = anxn + an-1xn-1 + … + a2x2 + a1x + a0 where n is a nonnegative integer and the numbers a0, a1, a2, …, an are constants called the coefficients of the polynomial. ...
CHAPTER IV NORMED LINEAR SPACES AND BANACH SPACES
... THEOREM 4.8. Let X be a Banach space, let Y be a normed linear space, let {Tn } be a sequence of elements of L(X, Y ), and suppose that {Tn } converges pointwise to a function T : X → Y. Then T is a continuous linear transformation of X into Y ; i.e., the pointwise limit of a sequence of continuous ...
... THEOREM 4.8. Let X be a Banach space, let Y be a normed linear space, let {Tn } be a sequence of elements of L(X, Y ), and suppose that {Tn } converges pointwise to a function T : X → Y. Then T is a continuous linear transformation of X into Y ; i.e., the pointwise limit of a sequence of continuous ...
FUNCTION SPACES – AND HOW THEY RELATE 1. Function
... 1.1. Why functions? This section is more about the gameplan and general philosophy that we’ll follow. The basic premise (which many may find disagreeable) is the following: We are interested in the functions of certain types from certain kinds of spaces, to R or C. We’re not interested in a function ...
... 1.1. Why functions? This section is more about the gameplan and general philosophy that we’ll follow. The basic premise (which many may find disagreeable) is the following: We are interested in the functions of certain types from certain kinds of spaces, to R or C. We’re not interested in a function ...