ANTIDERIVATIVES AND AREAS AND THINGS 1. Integration is
... Let’s pretend it’s a big scale and I can stretch the spring by 1 meter. Then I can graph the amount of force I apply in relation to the distance of stretch. It’s looks like this: ...
... Let’s pretend it’s a big scale and I can stretch the spring by 1 meter. Then I can graph the amount of force I apply in relation to the distance of stretch. It’s looks like this: ...
Concise
... points of this function. (d) Find the intervals where the graph of this function is concave up and concave down. (e) Sketch the graph of this function. Consider the function y= ...
... points of this function. (d) Find the intervals where the graph of this function is concave up and concave down. (e) Sketch the graph of this function. Consider the function y= ...
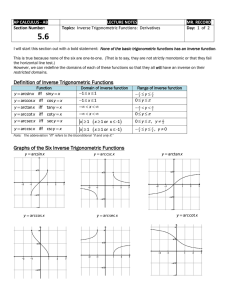
5.6: Inverse Trigonometric Functions: Differentiation
... LECTURE NOTES Topics: Inverse Trigonometric Functions: Derivatives - Inverse Trig Function Analyisis ...
... LECTURE NOTES Topics: Inverse Trigonometric Functions: Derivatives - Inverse Trig Function Analyisis ...
1 Introduction and Definitions 2 Example: The Area of a Circle
... in mind that this is just notation, so you shouldn’t be scared of it. However, I’ll try to avoid building up an excessive amount of notation since that can get confusing. This seems like an awfully di¢ cult de…nition to parse, so let me explain it. [Draw picture of a limit.] The de…nition says that ...
... in mind that this is just notation, so you shouldn’t be scared of it. However, I’ll try to avoid building up an excessive amount of notation since that can get confusing. This seems like an awfully di¢ cult de…nition to parse, so let me explain it. [Draw picture of a limit.] The de…nition says that ...
Dougherty Lecture 3
... where I is some interval, and f : I → R means that f inputs values in I and outputs values in R. (I will be the domain, and R will contain the range.) Thus C n (I) for a given interval I, or even C n (R) are natural domains of the operator L in (3). Note from calculus that if f k is defined and cont ...
... where I is some interval, and f : I → R means that f inputs values in I and outputs values in R. (I will be the domain, and R will contain the range.) Thus C n (I) for a given interval I, or even C n (R) are natural domains of the operator L in (3). Note from calculus that if f k is defined and cont ...
Only Connect - The Open University
... at a certain pace; a few hours later the message is countermanded so a second courier is sent out at a faster pace … will the second overtake the first in time? Meeting Point – Some people leave town A headed for town B and at the same time some people leave town B headed for town A on the same ro ...
... at a certain pace; a few hours later the message is countermanded so a second courier is sent out at a faster pace … will the second overtake the first in time? Meeting Point – Some people leave town A headed for town B and at the same time some people leave town B headed for town A on the same ro ...
Lecture 7: Recall f(x) = sgn(x) = f(x) = { 1 x > 0 −1 x 0 } Q: Does limx
... finite interval [a, b]. Then f has an absolute maximum and an absolute minimum on [a, b]. That is, there exist p, q ∈ [a, b] s.t. for all x ∈ [a, b], we have f (p) ≤ f (x) ≤ f (q). Max-Min theorem is (may be) false on open intervals (a, b): consider f (x) = x on (a, b) = (0, 1). Max-Min theorem is ( ...
... finite interval [a, b]. Then f has an absolute maximum and an absolute minimum on [a, b]. That is, there exist p, q ∈ [a, b] s.t. for all x ∈ [a, b], we have f (p) ≤ f (x) ≤ f (q). Max-Min theorem is (may be) false on open intervals (a, b): consider f (x) = x on (a, b) = (0, 1). Max-Min theorem is ( ...
Block 5 Stochastic & Dynamic Systems Lesson 14 – Integral Calculus
... Given a function f(x) that is continuous on the interval [a,b] we divide the interval into n subintervals of equal width, x, and from each interval choose a point, xi*. Then the definite integral of f(x) from a to b is ...
... Given a function f(x) that is continuous on the interval [a,b] we divide the interval into n subintervals of equal width, x, and from each interval choose a point, xi*. Then the definite integral of f(x) from a to b is ...
File
... part of the theorem is also important because it guarantees the existence of antiderivatives for continuous functions. The second part, sometimes called the second fundamental theorem of calculus, is that the definite integral of a function can be computed by using any one of its infinitely many ant ...
... part of the theorem is also important because it guarantees the existence of antiderivatives for continuous functions. The second part, sometimes called the second fundamental theorem of calculus, is that the definite integral of a function can be computed by using any one of its infinitely many ant ...