9.2 Solving with Exponents
... Objective: Solve equations with exponents using the odd root property and the even root property. Another type of equation we can solve is one with exponents. As you might expect we can clear exponents by using roots. This is done with very few unexpected results when the exponent is odd. We solve t ...
... Objective: Solve equations with exponents using the odd root property and the even root property. Another type of equation we can solve is one with exponents. As you might expect we can clear exponents by using roots. This is done with very few unexpected results when the exponent is odd. We solve t ...
Substitution method
... Additions – O(n) Multiplications by powers of two (actually left-shifts) – O(n) Four n/2-bit multiplications – xLyL, xLyR, xRyL, xRyR – with recursive calls. Our method for multiplying n-bit numbers starts by making recursive calls to multiply these four pairs of n/2-bit numbers (four sub-prob ...
... Additions – O(n) Multiplications by powers of two (actually left-shifts) – O(n) Four n/2-bit multiplications – xLyL, xLyR, xRyL, xRyR – with recursive calls. Our method for multiplying n-bit numbers starts by making recursive calls to multiply these four pairs of n/2-bit numbers (four sub-prob ...
Quadratic Equations Assignment_2
... Solving a quadratic equation means finding what value of the variable makes both sides of the equation equal. Solutions have the form x ______ . A quadratic equation can have two, one, or no solutions. There are three ways to solve a quadratic equation algebraically: 1. Factoring 2. Completing the ...
... Solving a quadratic equation means finding what value of the variable makes both sides of the equation equal. Solutions have the form x ______ . A quadratic equation can have two, one, or no solutions. There are three ways to solve a quadratic equation algebraically: 1. Factoring 2. Completing the ...
ODE - resnet.wm.edu
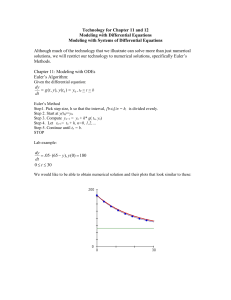
... which we call Euler’s method. Some examples can be found at http://www.sosmath.com/diffeq/first/numerical/numerical.html. The approximate solution is not a real solution, but it gives a set of data: (t0 , P0 ), (t1 , P1 ), (t2 , P2 ), · · · , (tn , Pn ), · · · which is close to the values of a real ...
... which we call Euler’s method. Some examples can be found at http://www.sosmath.com/diffeq/first/numerical/numerical.html. The approximate solution is not a real solution, but it gives a set of data: (t0 , P0 ), (t1 , P1 ), (t2 , P2 ), · · · , (tn , Pn ), · · · which is close to the values of a real ...
3.1: Derivative of a Function
... 1. Create scatter plot of data, use regression equation to get a graph of the derivative 2. Scatter plot of derivative points by numerically computing slopes between successive points #11 on worksheet ...
... 1. Create scatter plot of data, use regression equation to get a graph of the derivative 2. Scatter plot of derivative points by numerically computing slopes between successive points #11 on worksheet ...
2000 中華民國自動控制研討會徵文啟事
... fluid mechanics and gas dynamics. It is also related to a variety of applications such as traffic flow problems, continuous stochastic processes and the acoustic transmission in viscous medium. Many numerical methods for solving Burgers’ equation have been presented for decades. Aside from solving t ...
... fluid mechanics and gas dynamics. It is also related to a variety of applications such as traffic flow problems, continuous stochastic processes and the acoustic transmission in viscous medium. Many numerical methods for solving Burgers’ equation have been presented for decades. Aside from solving t ...
Document
... • Numerically – by completing a table and noting which x-value gives you the same y-value • Graphically – by graphing the equations and finding their point of intersection • Algebraically – by using properties of equality to solve the equations for one variable and then the other ...
... • Numerically – by completing a table and noting which x-value gives you the same y-value • Graphically – by graphing the equations and finding their point of intersection • Algebraically – by using properties of equality to solve the equations for one variable and then the other ...
Runge-Kutta Methods
... does not meet the user prescribed tolerance If this is the case, the step size should be decrased, yn is rejected and it’s to be computed again… ...
... does not meet the user prescribed tolerance If this is the case, the step size should be decrased, yn is rejected and it’s to be computed again… ...
Section 7.1
... If the system of equations being solved contains equations that can be easily graphed on a calculator, or are graphs that you can easily sketch (like linear equations), then we can solve the system by finding the point(s) at which all graphs in the system meet. This method gives an estimate to the s ...
... If the system of equations being solved contains equations that can be easily graphed on a calculator, or are graphs that you can easily sketch (like linear equations), then we can solve the system by finding the point(s) at which all graphs in the system meet. This method gives an estimate to the s ...
Minimum Weighted Residual Methods in Endogenous - cerge-ei
... Much of the current research in macroeconomics and mainly in neoclassical growth models is based on the intertemporal optimizing infinite-lived representative agent model. Solving these models via derivation of the first order necessary conditions by means of the Pontryagin Maximum Principle or the ...
... Much of the current research in macroeconomics and mainly in neoclassical growth models is based on the intertemporal optimizing infinite-lived representative agent model. Solving these models via derivation of the first order necessary conditions by means of the Pontryagin Maximum Principle or the ...
1 Numerical Solution to Quadratic Equations 2 Finding Square
... precision of the two original numbers. One might try to solve this problem by increasing the precision of the original numbers, but this is not a solution: For any finite precision storage, numbers that are close enough will be indistinguishable. There is no universal way to avoid loss of precision! ...
... precision of the two original numbers. One might try to solve this problem by increasing the precision of the original numbers, but this is not a solution: For any finite precision storage, numbers that are close enough will be indistinguishable. There is no universal way to avoid loss of precision! ...
Analyzing Cubic Functions
... Note that in the case of concave down, the derivative function is decreasing (not necessarily the graph itself). If the derivative function is decreasing, then the derivative of the derivative function must be negative. That is, the second derivative must be negative. A point at which concavity chan ...
... Note that in the case of concave down, the derivative function is decreasing (not necessarily the graph itself). If the derivative function is decreasing, then the derivative of the derivative function must be negative. That is, the second derivative must be negative. A point at which concavity chan ...
Java Programming class – Department of Network
... clause, then the compiler adds implicitly the code extend Object to the declaration for example Public class Employee { // code here ...
... clause, then the compiler adds implicitly the code extend Object to the declaration for example Public class Employee { // code here ...
1.1The Derivative and theTangent Line
... • The derivative is the formula which gives the slope of the tangent line at any point x for f(x) f ( x0 x) f ( x0 ) f '( x) lim x 0 x ...
... • The derivative is the formula which gives the slope of the tangent line at any point x for f(x) f ( x0 x) f ( x0 ) f '( x) lim x 0 x ...