
Numerical Solution of Fuzzy Polynomials by Newton
... Polynomials play a major role in various areas such as pure and applied mathematics, engineering and social sciences. In this paper we propose to find fuzzy roots of a fuzzy polynomial like A1 x A2 x 2 An x n A0 where x i , A j E 1 for (if exists). The set of all the fuzzy numbers is den ...
... Polynomials play a major role in various areas such as pure and applied mathematics, engineering and social sciences. In this paper we propose to find fuzzy roots of a fuzzy polynomial like A1 x A2 x 2 An x n A0 where x i , A j E 1 for (if exists). The set of all the fuzzy numbers is den ...
Java Software Structures, 4th Edition Exercise Solutions, Ch. 8
... Java Software Structures, 4th Edition ...
... Java Software Structures, 4th Edition ...
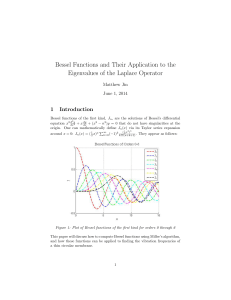
Bessel Functions and Their Application to the Eigenvalues of the
... The first task in this project was to compute Bessel functions, which was done using Miller’s downwards recurrence algorithm. The algorithm applies the recurrence relation Jn−1 (x) = 2n x Jn (x) − Jn+1 (x), where n is the order of Bessel function J—it computes Bessel functions in descending order fr ...
... The first task in this project was to compute Bessel functions, which was done using Miller’s downwards recurrence algorithm. The algorithm applies the recurrence relation Jn−1 (x) = 2n x Jn (x) − Jn+1 (x), where n is the order of Bessel function J—it computes Bessel functions in descending order fr ...
Developing And Comparing Numerical Methods For Computing The Inverse Fourier Transform Abstract
... The Fourier transform is (up to a negative sign and a scalar factor depending on the definition used) its own inverse. Thus, a numerical method that computes one, computes the other. However, with the exception of the Gaussian function ( e x ), functions and their Fourier transforms have different ...
... The Fourier transform is (up to a negative sign and a scalar factor depending on the definition used) its own inverse. Thus, a numerical method that computes one, computes the other. However, with the exception of the Gaussian function ( e x ), functions and their Fourier transforms have different ...
The Development of Algebraic Methods of Problem
... was reduced to a single process of eliminating one unknown within two given algebraic equations. Seki's ability to cope with such general contexts and questions was closely related to his use of adequate notations to represent polynomials and equations with literal coefficients (see Fig. 2). Seki's ...
... was reduced to a single process of eliminating one unknown within two given algebraic equations. Seki's ability to cope with such general contexts and questions was closely related to his use of adequate notations to represent polynomials and equations with literal coefficients (see Fig. 2). Seki's ...
user guide - Ruhr-Universität Bochum
... Once you have made your choices and entered your favourite parameters you press the Compute button to start the computations. The results will be depicted in the output part. Note that some examples, e.g. interpolation of a rational function, require additional input. This will be provided via addit ...
... Once you have made your choices and entered your favourite parameters you press the Compute button to start the computations. The results will be depicted in the output part. Note that some examples, e.g. interpolation of a rational function, require additional input. This will be provided via addit ...
Converting Mixed Numbers
... A “mixed number” is made up of a whole number and a fraction. An “improper fraction” is a fraction in which the numerator is greater than the denominator. ...
... A “mixed number” is made up of a whole number and a fraction. An “improper fraction” is a fraction in which the numerator is greater than the denominator. ...




















![[5pt] Fixed-point Convergence](http://s1.studyres.com/store/data/019993772_1-0637c0e3f0f8e20109c3fa6f5452261f-300x300.png)
