First-Order Predicate Logic (2) - Department of Computer Science
... F |= G versus X |= G • Note that F |= G or F |= ¬G, for every sentence G. Thus, we have complete information about the domain of discourse. There are many examples where X 6|= G and X 6|= ¬G. We have incomplete information. • F |= G means that G is true in the structure F . Checking whether this is ...
... F |= G versus X |= G • Note that F |= G or F |= ¬G, for every sentence G. Thus, we have complete information about the domain of discourse. There are many examples where X 6|= G and X 6|= ¬G. We have incomplete information. • F |= G means that G is true in the structure F . Checking whether this is ...
BEYOND ω-REGULAR LANGUAGES The notion of ω
... that does not use S-conditions is called a B-automaton; an automaton that does not use B-conditions is called an S-automaton. Theorem 1 ([3]). The complement of a language recognized by a nondeterministic Bautomaton is recognized by a nondeterministic S-automaton, and vice versa. The correspondence ...
... that does not use S-conditions is called a B-automaton; an automaton that does not use B-conditions is called an S-automaton. Theorem 1 ([3]). The complement of a language recognized by a nondeterministic Bautomaton is recognized by a nondeterministic S-automaton, and vice versa. The correspondence ...
Completeness or Incompleteness of Basic Mathematical Concepts
... truth values for all sentences of first-order arithmetic. That is, it implies each first-order sentence or its negation. In fact I think that the concept of the natural numbers has a stronger property than first-order completeness. I will discuss this property, which I call “full determinateness” in ...
... truth values for all sentences of first-order arithmetic. That is, it implies each first-order sentence or its negation. In fact I think that the concept of the natural numbers has a stronger property than first-order completeness. I will discuss this property, which I call “full determinateness” in ...
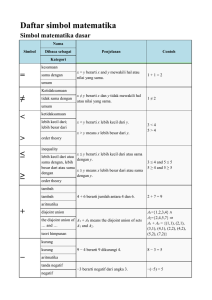
Daftar simbol matematika
... complex square root if z = r exp(iφ) is represented in polar the complex square coordinates with -π < φ ≤ π, then √z = √r √(-1) = i root of; square root ...
... complex square root if z = r exp(iφ) is represented in polar the complex square coordinates with -π < φ ≤ π, then √z = √r √(-1) = i root of; square root ...
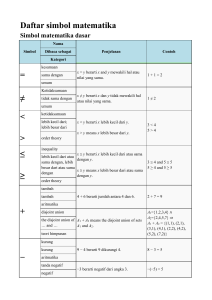
Daftar simbol matematika - Wikipedia bahasa Indonesia
... complex square root if z = r exp(iφ) is represented in polar the complex square coordinates with -π < φ ≤ π, then √z = √r √(-1) = i root of; square root ...
... complex square root if z = r exp(iφ) is represented in polar the complex square coordinates with -π < φ ≤ π, then √z = √r √(-1) = i root of; square root ...
Sequences and Series
... An arithmetic sequence is one where a constant value is added to each term to get the next term. example: {5, 7, 9, 11, …} A geometric sequence is one where a constant value is multiplied by each term to get the next term. example: {5, 10, 20, 40, …} EXAMPLE: Determine whether each of the following ...
... An arithmetic sequence is one where a constant value is added to each term to get the next term. example: {5, 7, 9, 11, …} A geometric sequence is one where a constant value is multiplied by each term to get the next term. example: {5, 10, 20, 40, …} EXAMPLE: Determine whether each of the following ...
MATH 2420 Discrete Mathematics
... A ⊆ B ⇔ ∀ x, if x ∈ A then x ∈ B. The definition of subset is rigid and inflexible. If any element in A does not appear in B then A cannot be a subset of B. That is: A 6⊆ B ⇔ ∃ x such that x ∈ A and x 6∈ B. Looking at the special sets above we have ...
... A ⊆ B ⇔ ∀ x, if x ∈ A then x ∈ B. The definition of subset is rigid and inflexible. If any element in A does not appear in B then A cannot be a subset of B. That is: A 6⊆ B ⇔ ∃ x such that x ∈ A and x 6∈ B. Looking at the special sets above we have ...
Solutions - TeacherWeb
... of the second month, $35 at the end of the third month, and so on. Ryan repaid the loan in 12 months. How much did the bike cost? How do you know your answer is correct? Ryan’s repayments form an arithmetic series with 12 terms, where the 1st term is his first payment, and the common difference is $ ...
... of the second month, $35 at the end of the third month, and so on. Ryan repaid the loan in 12 months. How much did the bike cost? How do you know your answer is correct? Ryan’s repayments form an arithmetic series with 12 terms, where the 1st term is his first payment, and the common difference is $ ...