Full tex
... transcendental number (see [1], [4], [6] and the references cited therein). Surprisingly, in comparison, very little attention has been paid to finding such sufficiency conditions in the case of infinite products. One such sufficiency condition is attributable to Cantor (see [3]) however some genera ...
... transcendental number (see [1], [4], [6] and the references cited therein). Surprisingly, in comparison, very little attention has been paid to finding such sufficiency conditions in the case of infinite products. One such sufficiency condition is attributable to Cantor (see [3]) however some genera ...
Full text
... systems theory of obtaining new functions Q(n) from the known ones so that many more Q(n) can be constructed (see, e.g., Theorem 4). Finally, in [8], Lin only considered the numbers of period-/! points for iterated maps. He did not mention the numbers of symmetric period-(2«) points. Therefore, we a ...
... systems theory of obtaining new functions Q(n) from the known ones so that many more Q(n) can be constructed (see, e.g., Theorem 4). Finally, in [8], Lin only considered the numbers of period-/! points for iterated maps. He did not mention the numbers of symmetric period-(2«) points. Therefore, we a ...
Generating Functions 1 Introduction 2 Useful Facts
... 3. (USAMO 1996, weakened) Determine (with proof) whether there is a subset X of the nonnegative integers with the following property: for any integer n there is exactly one solution of a + 2b = n with a, b ∈ X. 4. (USAMO 1996) Determine (with proof) whether there is a subset X of the integers with t ...
... 3. (USAMO 1996, weakened) Determine (with proof) whether there is a subset X of the nonnegative integers with the following property: for any integer n there is exactly one solution of a + 2b = n with a, b ∈ X. 4. (USAMO 1996) Determine (with proof) whether there is a subset X of the integers with t ...
journal of number theory 13, 446
... often more interesting to consider the following property . Call a sequence S strongly complete if it remains complete after removal of any finite number of terms . Although strong completeness is a very interesting property and will figure considerably in what follows, we will be primarily concerne ...
... often more interesting to consider the following property . Call a sequence S strongly complete if it remains complete after removal of any finite number of terms . Although strong completeness is a very interesting property and will figure considerably in what follows, we will be primarily concerne ...
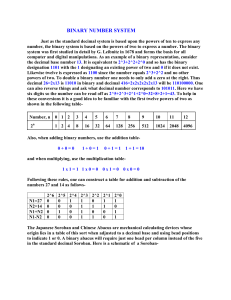
binary number system
... Subtraction in binary makes use of the subtraction table: 1-0=1, 1-1=0, 0-0=0, and 0-1=1 borrow 1. Thus 1100-101=111 and 101001-1110=11011. Division in binary is a bit more complicated and best treated as the inverse of multiplication. As an example consider the division 6/3=2 or its equivalent mult ...
... Subtraction in binary makes use of the subtraction table: 1-0=1, 1-1=0, 0-0=0, and 0-1=1 borrow 1. Thus 1100-101=111 and 101001-1110=11011. Division in binary is a bit more complicated and best treated as the inverse of multiplication. As an example consider the division 6/3=2 or its equivalent mult ...
pdf
... Although each of these instances was studied separately, there are some striking similarities. It turns out that the key to progress in all of them is the identification of a suitable class of language models that characterize the equational theory of the system. A language model is a structure in w ...
... Although each of these instances was studied separately, there are some striking similarities. It turns out that the key to progress in all of them is the identification of a suitable class of language models that characterize the equational theory of the system. A language model is a structure in w ...
a basis for a mathematical theory of computation
... of information. The present paper contains no information about this. The present paper is divided into two sections. The first contains several descriptive formalisms with a few examples of their use, and the second contains what little theory we have that enables us to prove the equivalence of com ...
... of information. The present paper contains no information about this. The present paper is divided into two sections. The first contains several descriptive formalisms with a few examples of their use, and the second contains what little theory we have that enables us to prove the equivalence of com ...
Elementary Number Theory
... Number theory is the branch of mathematics concerned with the properties of the positive integers, such as divisibility, prime numbers, and so forth. It is an ancient subject: four volumes of Euclid’s Elements were devoted entirely to number theory, and Greek mathematicians were arguably as interest ...
... Number theory is the branch of mathematics concerned with the properties of the positive integers, such as divisibility, prime numbers, and so forth. It is an ancient subject: four volumes of Euclid’s Elements were devoted entirely to number theory, and Greek mathematicians were arguably as interest ...
Normality and nonnormality of mathematical
... A result for algebraic numbers If x is algebraic of degree d > 1, then its binary expansion through position n must have at least C n1/d 1-bits, for all sufficiently large n and some C that depends on x. Example: The first n binary digits of sqrt(2) must have at least sqrt(n) ones. For the special ...
... A result for algebraic numbers If x is algebraic of degree d > 1, then its binary expansion through position n must have at least C n1/d 1-bits, for all sufficiently large n and some C that depends on x. Example: The first n binary digits of sqrt(2) must have at least sqrt(n) ones. For the special ...
Boolean Logic - Programming Systems Lab
... ideas. There are different interpretations of boolean logic. The canonical interpretation is concerned with operations on a two-valued set. The algebraic interpretation relates boolean logic with operations on power sets. We will focus on semantic equivalence of boolean expressions and study decisio ...
... ideas. There are different interpretations of boolean logic. The canonical interpretation is concerned with operations on a two-valued set. The algebraic interpretation relates boolean logic with operations on power sets. We will focus on semantic equivalence of boolean expressions and study decisio ...
Chapter 1: Sets, Operations and Algebraic Language
... given set and closes the door. No other numbers are in the room. Then the teacher turns on an “operations” machine (egs. Add, subtract, multiply, or divide). If the machine can run forever with just the numbers in the room, the set of numbers is closed for that operation. If the machine ever creates ...
... given set and closes the door. No other numbers are in the room. Then the teacher turns on an “operations” machine (egs. Add, subtract, multiply, or divide). If the machine can run forever with just the numbers in the room, the set of numbers is closed for that operation. If the machine ever creates ...