Propositional Logic What is logic? Propositions Negation
... – If p is the proposition “ISE students love logic”, and q is the proposition “ISE students are crazy”, then – p ∧ q is the proposition “ISE students love logic and are crazy” – p ∨ q is the proposition “ISE students either love logic, or are crazy, or both” Note the syntax is different to that used ...
... – If p is the proposition “ISE students love logic”, and q is the proposition “ISE students are crazy”, then – p ∧ q is the proposition “ISE students love logic and are crazy” – p ∨ q is the proposition “ISE students either love logic, or are crazy, or both” Note the syntax is different to that used ...
Lecturecise 19 Proofs and Resolution Compactness for
... then interpretation makes it true. Moreover, all other formulas in T are propositional variables set to true, so the interpretation makes T true. Thus, we see that the inductively proved statement holds even in this case. What the infinite formula D breaks is the second part, which, from the existen ...
... then interpretation makes it true. Moreover, all other formulas in T are propositional variables set to true, so the interpretation makes T true. Thus, we see that the inductively proved statement holds even in this case. What the infinite formula D breaks is the second part, which, from the existen ...
Dear Parents
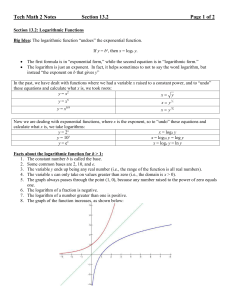
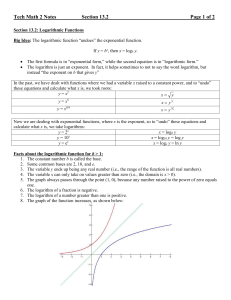
... Recursive Definition: Gives the 1st term and a formula for how a specific term ( nth term) relates to a previous term [(n-1) th term.] Relation: A rule that gives an output number for every valid input number Sequence: an ordered set of numbers or items ...
... Recursive Definition: Gives the 1st term and a formula for how a specific term ( nth term) relates to a previous term [(n-1) th term.] Relation: A rule that gives an output number for every valid input number Sequence: an ordered set of numbers or items ...
Lecture 1:
... element of the range. Def: Domain: A non-empty set which is mapped to another set by a function Def: Range: A non-empty set which is mapped to another set by a function ...
... element of the range. Def: Domain: A non-empty set which is mapped to another set by a function Def: Range: A non-empty set which is mapped to another set by a function ...
Incompleteness - the UNC Department of Computer Science
... that human mathematical understanding cannot be encapsulated in any (knowably sound) computational procedure. This has the implication that there is something involved in human understanding that lies beyond the actions of any computer. Understanding is a particular manifestation of human consciousn ...
... that human mathematical understanding cannot be encapsulated in any (knowably sound) computational procedure. This has the implication that there is something involved in human understanding that lies beyond the actions of any computer. Understanding is a particular manifestation of human consciousn ...
Principia Mathematica

The Principia Mathematica is a three-volume work on the foundations of mathematics, written by Alfred North Whitehead and Bertrand Russell and published in 1910, 1912, and 1913. In 1927, it appeared in a second edition with an important Introduction To the Second Edition, an Appendix A that replaced ✸9 and an all-new Appendix C.PM, as it is often abbreviated, was an attempt to describe a set of axioms and inference rules in symbolic logic from which all mathematical truths could in principle be proven. As such, this ambitious project is of great importance in the history of mathematics and philosophy, being one of the foremost products of the belief that such an undertaking may be achievable. However, in 1931, Gödel's incompleteness theorem proved definitively that PM, and in fact any other attempt, could never achieve this lofty goal; that is, for any set of axioms and inference rules proposed to encapsulate mathematics, either the system must be inconsistent, or there must in fact be some truths of mathematics which could not be deduced from them.One of the main inspirations and motivations for PM was the earlier work of Gottlob Frege on logic, which Russell discovered allowed for the construction of paradoxical sets. PM sought to avoid this problem by ruling out the unrestricted creation of arbitrary sets. This was achieved by replacing the notion of a general set with the notion of a hierarchy of sets of different 'types', a set of a certain type only allowed to contain sets of strictly lower types. Contemporary mathematics, however, avoids paradoxes such as Russell's in less unwieldy ways, such as the system of Zermelo–Fraenkel set theory.PM is not to be confused with Russell's 1903 Principles of Mathematics. PM states: ""The present work was originally intended by us to be comprised in a second volume of Principles of Mathematics... But as we advanced, it became increasingly evident that the subject is a very much larger one than we had supposed; moreover on many fundamental questions which had been left obscure and doubtful in the former work, we have now arrived at what we believe to be satisfactory solutions.""The Modern Library placed it 23rd in a list of the top 100 English-language nonfiction books of the twentieth century.