Remarkable Theorem
... In a precalculus course, we gave the definition of ay if a > 0 and y is any rational number. But we did not define ay if y is irrational because this would have been an extremely difficult task without the use of calculus. We are now in a position where it is easy to define irrational exponents, and ...
... In a precalculus course, we gave the definition of ay if a > 0 and y is any rational number. But we did not define ay if y is irrational because this would have been an extremely difficult task without the use of calculus. We are now in a position where it is easy to define irrational exponents, and ...
A → (B → A)
... Assume V(B) = false; B came from Ei and Ei → B (which is Ej) If V(Ei) = true then V(Ej) = false and if V(Ei) = false then V(Ej) = true This means one of Ei and Ej is not an axiom or hypothesis This means that the false formula has to be the result of MP between Em and En which come before Ei (or Ej) ...
... Assume V(B) = false; B came from Ei and Ei → B (which is Ej) If V(Ei) = true then V(Ej) = false and if V(Ei) = false then V(Ej) = true This means one of Ei and Ej is not an axiom or hypothesis This means that the false formula has to be the result of MP between Em and En which come before Ei (or Ej) ...
answers, in pdf - People @ EECS at UC Berkeley
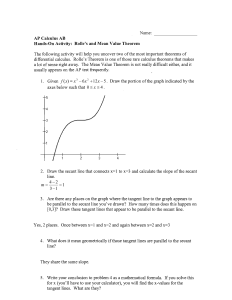
... Solution The length of the subintervals are ∆x = 1. Reading four values at the left end points, we get f (3) = 8, f (4) = 7, f (5) = 6, f (6) = 4. So the Riemann sum is ∆x[f (3) + f (4) + f (5) + f (6)] = 8 + 7 + 6 + 4 = 25 To draw approximating rectangles, sketch 4 rectangles with width 1; The firs ...
... Solution The length of the subintervals are ∆x = 1. Reading four values at the left end points, we get f (3) = 8, f (4) = 7, f (5) = 6, f (6) = 4. So the Riemann sum is ∆x[f (3) + f (4) + f (5) + f (6)] = 8 + 7 + 6 + 4 = 25 To draw approximating rectangles, sketch 4 rectangles with width 1; The firs ...
tan(x) - The Math Forum @ Drexel
... a given arc length and its corresponding chord length, and in problems involving how deep a log of a certain specific gravity and a specific diameter sinks in water. ...
... a given arc length and its corresponding chord length, and in problems involving how deep a log of a certain specific gravity and a specific diameter sinks in water. ...
Solution - Math TAMU
... asymptotes when x = ±1, and the x-axis is a horizontal asymptote when x → ±∞. In order for the graph to have negative slope everywhere on its domain and to have the origin as its only inflection point, the graph must look something like the following figure. ...
... asymptotes when x = ±1, and the x-axis is a horizontal asymptote when x → ±∞. In order for the graph to have negative slope everywhere on its domain and to have the origin as its only inflection point, the graph must look something like the following figure. ...
x dx
... If there no are secant factors and the power of the tangent is even and positive, convert a tangent-squared factor to a secant-squared factor. Then expand and ...
... If there no are secant factors and the power of the tangent is even and positive, convert a tangent-squared factor to a secant-squared factor. Then expand and ...
Microsoft Word Format
... Guidelines for Analyzing the Graph of a Function: 1. Find the x- and y-intercepts (set x and y to zero and solve for the other) 2. Find the vertical and horizontal asymptotes a. Vertical: set denominator equal to zero b. Horizontal: Lim f(x) = L (divide by highest power on denominator) x→ ∞ 3. Find ...
... Guidelines for Analyzing the Graph of a Function: 1. Find the x- and y-intercepts (set x and y to zero and solve for the other) 2. Find the vertical and horizontal asymptotes a. Vertical: set denominator equal to zero b. Horizontal: Lim f(x) = L (divide by highest power on denominator) x→ ∞ 3. Find ...
Lesson 18 – Finding Indefinite and Definite Integrals 1 Math 1314
... Working with Riemann sums can be quite time consuming, and at best we get a good approximation. In an area problem, we want an exact area, not an approximation. The definite integral will give us the exact area, so we need to see how we can find this. We need to start by finding an antiderivative: A ...
... Working with Riemann sums can be quite time consuming, and at best we get a good approximation. In an area problem, we want an exact area, not an approximation. The definite integral will give us the exact area, so we need to see how we can find this. We need to start by finding an antiderivative: A ...
dx - TaMATHawis!
... What you are finding: You are looking at problems in the form of " f (t) dt . This is asking for the rate dx a of change with respect to x of the accumulation function starting at some constant (which is irrelevant) and ending at that variable x. It is important to understand that this expression is ...
... What you are finding: You are looking at problems in the form of " f (t) dt . This is asking for the rate dx a of change with respect to x of the accumulation function starting at some constant (which is irrelevant) and ending at that variable x. It is important to understand that this expression is ...
History of calculus
Calculus, known in its early history as infinitesimal calculus, is a mathematical discipline focused on limits, functions, derivatives, integrals, and infinite series. Isaac Newton and Gottfried Leibniz independently invented calculus in the mid-17th century. However, each inventor claimed that the other one stole his work in a bitter dispute that continued until the end of their lives.