A new proof of the maximal monotonicity of
... analytic, while that of [6, Theorem 29.4, pp. 116–118] is much harder and has a much more geometric feel. On the other hand, this latter argument leads to the more general results in the later parts of [6, Chapter VII]. We now know that all these more general results can be established using the res ...
... analytic, while that of [6, Theorem 29.4, pp. 116–118] is much harder and has a much more geometric feel. On the other hand, this latter argument leads to the more general results in the later parts of [6, Chapter VII]. We now know that all these more general results can be established using the res ...
Section 1.4: Combinations of Functions
... The Fact tells us that between any two places where the y = h(x) = 1 (because x is rational) there is a place where y = h(x) is 2 because there is an irrational number between any two distinct rational numbers. Similarly, between any two places where y = h(x) = 2 (because x is irrational) there is a ...
... The Fact tells us that between any two places where the y = h(x) = 1 (because x is rational) there is a place where y = h(x) is 2 because there is an irrational number between any two distinct rational numbers. Similarly, between any two places where y = h(x) = 2 (because x is irrational) there is a ...
Higher–Dimensional Chain Rules I. Introduction. The one
... Thus, the limit of quantity (A) is exactly the right-hand side of Equation (4). To prove the theorem, then, I must show that the limit of quantity (B) is zero. Step 4: Evaluating the limit of quantity (B). Assume, for all h 6= 0, that h xh , yh i 6= h x0 , y0 i1 , so that one can multiply and divide ...
... Thus, the limit of quantity (A) is exactly the right-hand side of Equation (4). To prove the theorem, then, I must show that the limit of quantity (B) is zero. Step 4: Evaluating the limit of quantity (B). Assume, for all h 6= 0, that h xh , yh i 6= h x0 , y0 i1 , so that one can multiply and divide ...
Section 1.5: Mathematical Language
... calculus you will have to master some techniques, but, more importantly, you will have to understand ideas and be able to work with the ideas in words and pictures -- very clear words and pictures. You also need to understand some of the common linguistic constructions used in mathematics. In this s ...
... calculus you will have to master some techniques, but, more importantly, you will have to understand ideas and be able to work with the ideas in words and pictures -- very clear words and pictures. You also need to understand some of the common linguistic constructions used in mathematics. In this s ...
Integral Tables and Integrals Using CAS
... Reference Pages 4 through 8 at the back of the book), a small number compared to reference books devoted solely to integral tables. Integral tables provide yet another way to help evaluate integrals. Using the tables, your goals should be to: identify patterns in the integral you are attempting to ...
... Reference Pages 4 through 8 at the back of the book), a small number compared to reference books devoted solely to integral tables. Integral tables provide yet another way to help evaluate integrals. Using the tables, your goals should be to: identify patterns in the integral you are attempting to ...
Calculus 1 Syllabus
... of Woolsthorpe to escape the worst ravages of the Black Plague. At the age of 23, while relaxing on his mother's farm, Newton, by his own account, saw an apple falling from a tree and he asked a simple question, “If apple fall, does the moon also fall”. He invented calculus to solve this falling moo ...
... of Woolsthorpe to escape the worst ravages of the Black Plague. At the age of 23, while relaxing on his mother's farm, Newton, by his own account, saw an apple falling from a tree and he asked a simple question, “If apple fall, does the moon also fall”. He invented calculus to solve this falling moo ...
Calculus: A Marxist approach - Australian Mathematical Society
... tried in [a] characteristic way to straighten out the difficulties for himself’ [16, p. 187]. Kennedy agrees that Marx was ‘interested in mathematics for its own sake’ [4, p. 306]. This view is supported by Marx himself to some extent; in a letter to Engels on 6 July 1863, Marx wrote: ‘My spare time i ...
... tried in [a] characteristic way to straighten out the difficulties for himself’ [16, p. 187]. Kennedy agrees that Marx was ‘interested in mathematics for its own sake’ [4, p. 306]. This view is supported by Marx himself to some extent; in a letter to Engels on 6 July 1863, Marx wrote: ‘My spare time i ...
this document - KSU Web Home
... In practice, …nding A using the de…nition is very di¢ cult. First, the expression resulting from the sum is usually very complicated. Then, we have to take its limit as n approaches in…nity. We will not spend any more time on it, but you should remember the formula. ...
... In practice, …nding A using the de…nition is very di¢ cult. First, the expression resulting from the sum is usually very complicated. Then, we have to take its limit as n approaches in…nity. We will not spend any more time on it, but you should remember the formula. ...
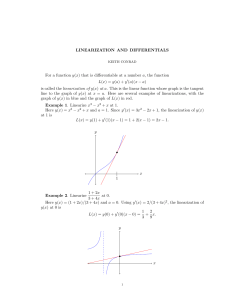
LINEARIZATION AND DIFFERENTIALS For a function y(x) that is
... 1 + x at 0 gave us an estimate of the cube root of 1729.03 that is correct to 5 digits after the decimal point. This cube root calculation is based on a story the physicist Richard Feynman told about being challenged to make calculations with pencil and paper against an abacus salesman to see who wo ...
... 1 + x at 0 gave us an estimate of the cube root of 1729.03 that is correct to 5 digits after the decimal point. This cube root calculation is based on a story the physicist Richard Feynman told about being challenged to make calculations with pencil and paper against an abacus salesman to see who wo ...
(pdf)
... and possibly more. Now, since R and Φ are elementarily equivalent, any theorem, relation, or operation have the same properties in both R and φ. Because of the isomorphic function between these two structures, properties, operations, and relations are directly comparable from R to φ, and back from t ...
... and possibly more. Now, since R and Φ are elementarily equivalent, any theorem, relation, or operation have the same properties in both R and φ. Because of the isomorphic function between these two structures, properties, operations, and relations are directly comparable from R to φ, and back from t ...
File
... 6. Let F t represent a bacteria population which is 4 million at time t = 0. After t hours, the population is growing at an instantaneous rate of 2t million bacteria per hour. Find the total increase in the bacteria population during the first three hours, and find the population at t = 3 hours. ...
... 6. Let F t represent a bacteria population which is 4 million at time t = 0. After t hours, the population is growing at an instantaneous rate of 2t million bacteria per hour. Find the total increase in the bacteria population during the first three hours, and find the population at t = 3 hours. ...
DEFINITE INTEGRALS
... shaded region in Fig.27.3. Now the problem is to find the area of the shaded region. In order to solve this problem, we consider three special cases of f (x) as rectangular region , triangular region and trapezoidal region. The area of these regions = base × average height In general for any functio ...
... shaded region in Fig.27.3. Now the problem is to find the area of the shaded region. In order to solve this problem, we consider three special cases of f (x) as rectangular region , triangular region and trapezoidal region. The area of these regions = base × average height In general for any functio ...
History of calculus
Calculus, known in its early history as infinitesimal calculus, is a mathematical discipline focused on limits, functions, derivatives, integrals, and infinite series. Isaac Newton and Gottfried Leibniz independently invented calculus in the mid-17th century. However, each inventor claimed that the other one stole his work in a bitter dispute that continued until the end of their lives.