PREDICATE LOGIC
... bound is said to be free. Later, we will see that the same variable can occur both bound and free in an expression. For this reason, it is important to also indicate the position of the variable in question. Example 1.11. Find the bound and free variables in ∀ z (P (z) ∧ Q(x)) ∨ ∃ y Q(y). Solution: ...
... bound is said to be free. Later, we will see that the same variable can occur both bound and free in an expression. For this reason, it is important to also indicate the position of the variable in question. Example 1.11. Find the bound and free variables in ∀ z (P (z) ∧ Q(x)) ∨ ∃ y Q(y). Solution: ...
22c:145 Artificial Intelligence
... Propositional Logic An inference system I for PL is a procedure that given a set Γ = {α1 , . . . , αm } of sentences and a sentence ϕ, may reply “yes”, “no”, or runs forever. If I replies positively to input (Γ, ϕ), we say that Γ derives ϕ in I , a and write Γ /I ϕ Intuitively, I should be such that ...
... Propositional Logic An inference system I for PL is a procedure that given a set Γ = {α1 , . . . , αm } of sentences and a sentence ϕ, may reply “yes”, “no”, or runs forever. If I replies positively to input (Γ, ϕ), we say that Γ derives ϕ in I , a and write Γ /I ϕ Intuitively, I should be such that ...
Version 1.5 - Trent University
... and determine their truth. The real fun lies in the relationship between interpretation of statements, truth, and reasoning. This volume develops the basics of two kinds of formal logical systems, propositional logic and first-order logic. Propositional logic attempts to make precise the relationshi ...
... and determine their truth. The real fun lies in the relationship between interpretation of statements, truth, and reasoning. This volume develops the basics of two kinds of formal logical systems, propositional logic and first-order logic. Propositional logic attempts to make precise the relationshi ...
Second-Order Logic of Paradox
... the familiar “truth tables” of Kleene’s (strong) 3-valued logic [9, §64], but whereas for Kleene (thinking of the “middle value” as truth-valuelessness) only the top value (True) is designated, for Priest the top two values are both designated. As Priest might say: a formula which is both true and f ...
... the familiar “truth tables” of Kleene’s (strong) 3-valued logic [9, §64], but whereas for Kleene (thinking of the “middle value” as truth-valuelessness) only the top value (True) is designated, for Priest the top two values are both designated. As Priest might say: a formula which is both true and f ...
The G.U.E.S.S. Format
... Let x represent the number of apples eaten. x= 7-4 x= 3 Therefore, three apples were eaten. ...
... Let x represent the number of apples eaten. x= 7-4 x= 3 Therefore, three apples were eaten. ...
Boolean Algebra and Logic Gates
... be expressed in a compact form by listing the decimal value corresponding to the min term for which the function value is 1. ◦ As an example, the truth table of a three-variable function is shown below. Three variables, each of which can take the values 0 or 1, yield eight possible combinations of v ...
... be expressed in a compact form by listing the decimal value corresponding to the min term for which the function value is 1. ◦ As an example, the truth table of a three-variable function is shown below. Three variables, each of which can take the values 0 or 1, yield eight possible combinations of v ...
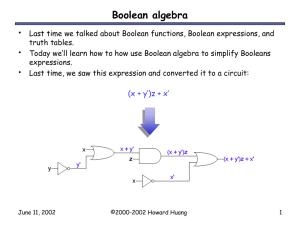
Boolean Algebra
... A sum of products (SOP) expression is characterized by: – There are only OR (sum) operations at the “outermost” level. – Each term in the sum must be a product of literals. For example: f(x,y,z) = y’ + x’yz’ + xz ...
... A sum of products (SOP) expression is characterized by: – There are only OR (sum) operations at the “outermost” level. – Each term in the sum must be a product of literals. For example: f(x,y,z) = y’ + x’yz’ + xz ...
Hilbert Calculus
... Let S be a set of formulas - also called hypothesis - and let F be a formula. We write S ⊢ F and say that F is a syntactic consequence of S in Hilbert Calculus if one of these conditions holds: ...
... Let S be a set of formulas - also called hypothesis - and let F be a formula. We write S ⊢ F and say that F is a syntactic consequence of S in Hilbert Calculus if one of these conditions holds: ...