Theorem 6.3.1 Angle Sum Theorem for Hyperbolic Geometry
... The points of the circle that encloses the disc are NOT points of Hyperbolic Geometry nor are any points exterior to the circle. Lines are arcs of orthogonal circles to the given circle. A circle that is orthogonal to the given circle intersects it in two points and tangent lines to each circle at t ...
... The points of the circle that encloses the disc are NOT points of Hyperbolic Geometry nor are any points exterior to the circle. Lines are arcs of orthogonal circles to the given circle. A circle that is orthogonal to the given circle intersects it in two points and tangent lines to each circle at t ...
Connecting the Data: Geometry and Measurement
... width of 10 feet. The length was increased by 50%, and the width was decreased by 50% to form a new garden. How does the area of the new garden compare to the area of the original garden? The area of the new garden is ...
... width of 10 feet. The length was increased by 50%, and the width was decreased by 50% to form a new garden. How does the area of the new garden compare to the area of the original garden? The area of the new garden is ...
Holt Geometry 4-4
... of corresponding parts were congruent. (3 pair of congruent sides and 3 pair of congruent angles) ...
... of corresponding parts were congruent. (3 pair of congruent sides and 3 pair of congruent angles) ...
Zanesville City Schools
... Use coordinates to prove simple geometric theorems algebraically. G-GPE.4-7 Prove geometric G-CO.8 Explain how the criteria for triangle congruence (ASA, SAS, and theorems. SSS) follow from the definition of G-CO.9-11 ...
... Use coordinates to prove simple geometric theorems algebraically. G-GPE.4-7 Prove geometric G-CO.8 Explain how the criteria for triangle congruence (ASA, SAS, and theorems. SSS) follow from the definition of G-CO.9-11 ...
M/J Mathematics 1 2002050
... Determine the center of a given circle. Given three points not on a line, construct the circle that passes through them. Construct tangents to circles. Circumscribe and inscribe circles about and within triangles and regular polygons. ...
... Determine the center of a given circle. Given three points not on a line, construct the circle that passes through them. Construct tangents to circles. Circumscribe and inscribe circles about and within triangles and regular polygons. ...
4.5 Triangle Congruence ASA. AAS
... Determine if you can use the HL Congruence Theorem to prove the triangles congruent. If not, tell what else you need to know. According to the diagram, the triangles are right triangles that share one leg. It is given that the hypotenuses are congruent, therefore the triangles are congruent by HL. H ...
... Determine if you can use the HL Congruence Theorem to prove the triangles congruent. If not, tell what else you need to know. According to the diagram, the triangles are right triangles that share one leg. It is given that the hypotenuses are congruent, therefore the triangles are congruent by HL. H ...
File
... inputs and give other points as outputs. Compare transformations that preserve distance and angle to those that do not. HSG-CO.A.3 Given a rectangle, parallelogram, trapezoid, or regular polygon, describe the rotations and reflections that carry it onto itself HSG-CO.A.5 Given a geometric figure and ...
... inputs and give other points as outputs. Compare transformations that preserve distance and angle to those that do not. HSG-CO.A.3 Given a rectangle, parallelogram, trapezoid, or regular polygon, describe the rotations and reflections that carry it onto itself HSG-CO.A.5 Given a geometric figure and ...
2.2 Deductive Reasoning powerpoint
... Conditional statements can be written in “if-then” form to emphasize which part is the hypothesis and which is the conclusion. ...
... Conditional statements can be written in “if-then” form to emphasize which part is the hypothesis and which is the conclusion. ...
Ag_mod05_les03 congruent parts of congruent triangles
... Triangle Congruence: CPCTC Check It Out! Example 1 A landscape architect sets up the triangles shown in the figure to find the distance JK across a pond. What is JK? One angle pair is congruent, because they are vertical angles. ...
... Triangle Congruence: CPCTC Check It Out! Example 1 A landscape architect sets up the triangles shown in the figure to find the distance JK across a pond. What is JK? One angle pair is congruent, because they are vertical angles. ...
13b.pdf
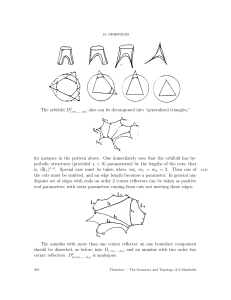
... With this definition, natural fibrations over manifolds give rise to natural fibrations over orbifolds. The tangent sphere bundle T S(M) is the fibration over M with fiber the sphere of rays through O in T (M). When M is Riemannian, this is identified with the unit tangent bundle T1 (M). Proposition ...
... With this definition, natural fibrations over manifolds give rise to natural fibrations over orbifolds. The tangent sphere bundle T S(M) is the fibration over M with fiber the sphere of rays through O in T (M). When M is Riemannian, this is identified with the unit tangent bundle T1 (M). Proposition ...
HONORS GEOMETRY A Semester Exam Review
... The measure of each interior angle of a regular polygon is 120o. How many sides does the polygon have? ...
... The measure of each interior angle of a regular polygon is 120o. How many sides does the polygon have? ...