On the number e, its irrationality, and factorials
... number of times. Therefore there can be no integers a and b for which 2 = a/b. All proofs that a number r is irrational follow this pattern of logic, called proof by contradiction: To prove that r is irrational we assume r = a/b for some integers a and b and then show (somehow) that this assumption ...
... number of times. Therefore there can be no integers a and b for which 2 = a/b. All proofs that a number r is irrational follow this pattern of logic, called proof by contradiction: To prove that r is irrational we assume r = a/b for some integers a and b and then show (somehow) that this assumption ...
MATH M16A: Applied Calculus Course Objectives (COR) • Evaluate
... Evaluate the limit of a function, including one-sided and two-sided, using numerical and algebraic techniques and the properties of limits. Determine whether a function is continuous or discontinuous at a point. Calculate the derivative of an algebraic function using the formal definition of the der ...
... Evaluate the limit of a function, including one-sided and two-sided, using numerical and algebraic techniques and the properties of limits. Determine whether a function is continuous or discontinuous at a point. Calculate the derivative of an algebraic function using the formal definition of the der ...
Chem 11 Empirical and Molecular Formulas Empirical formula
... Analysis of an unknown sample to determine the percent composition of elements can be used to find the empirical formula. However, there can be many compounds that have the same empirical formula: Ex: Benzene, C6H6 and acetylene, C2H2 are very different substances but both have the empirical formula ...
... Analysis of an unknown sample to determine the percent composition of elements can be used to find the empirical formula. However, there can be many compounds that have the same empirical formula: Ex: Benzene, C6H6 and acetylene, C2H2 are very different substances but both have the empirical formula ...
2015_Spring_M140_TopicsList
... There will be a review session by the Calculus I tutor on Monday, May 18. This review session will cover the practice problems found in this directory. The following Topic list was created by Prof. Cunningham. Please notice the problems listed. Limits ...
... There will be a review session by the Calculus I tutor on Monday, May 18. This review session will cover the practice problems found in this directory. The following Topic list was created by Prof. Cunningham. Please notice the problems listed. Limits ...
Math 111 - Solution of Test 1 Problem 1. The graph of y = f(x) is
... Problem 4. Find the formula of the function f(x) that best fits the data in the following table: x ...
... Problem 4. Find the formula of the function f(x) that best fits the data in the following table: x ...
9.3. Itô`s formula. First I stated the theorem. Then I did a simple
... But we have t/δt terms in this sum so the sum is t = 2(δt)2 = 2tδt δt which converges to zero as δt → 0. This proves: Var(#W $t ) = 0. ...
... But we have t/δt terms in this sum so the sum is t = 2(δt)2 = 2tδt δt which converges to zero as δt → 0. This proves: Var(#W $t ) = 0. ...
Dated 1/22/01
... and an identity which isn’t too hard to derive directly: Fk Fn−1 + Fk+1 Fn = Fn Fk−1 + Fn+1 Fk , Here are three questions I won’t answer, but you might want to: (i) What is a “good” formula for Fn1 +n2 +n3 ? There are two metrics for “good”. One is that you want a symmetric formula, the other is tha ...
... and an identity which isn’t too hard to derive directly: Fk Fn−1 + Fk+1 Fn = Fn Fk−1 + Fn+1 Fk , Here are three questions I won’t answer, but you might want to: (i) What is a “good” formula for Fn1 +n2 +n3 ? There are two metrics for “good”. One is that you want a symmetric formula, the other is tha ...
2. 2 2 = 1 1 n i=1 n−1 i=1
... only if x1 = x/b, and the remaining xi are defined recursively by xi+1 = ri xi . ...
... only if x1 = x/b, and the remaining xi are defined recursively by xi+1 = ri xi . ...
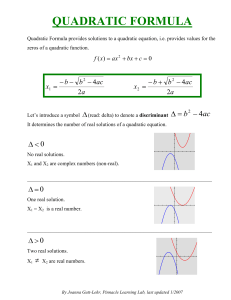
9.6 The Quadratic Formula and the Discriminant.notebook
... 9.6 The Quadratic Formula and the Discriminant.notebook ...
... 9.6 The Quadratic Formula and the Discriminant.notebook ...
Automatic differentiation

In mathematics and computer algebra, automatic differentiation (AD), also called algorithmic differentiation or computational differentiation, is a set of techniques to numerically evaluate the derivative of a function specified by a computer program. AD exploits the fact that every computer program, no matter how complicated, executes a sequence of elementary arithmetic operations (addition, subtraction, multiplication, division, etc.) and elementary functions (exp, log, sin, cos, etc.). By applying the chain rule repeatedly to these operations, derivatives of arbitrary order can be computed automatically, accurately to working precision, and using at most a small constant factor more arithmetic operations than the original program.Automatic differentiation is not: Symbolic differentiation, nor Numerical differentiation (the method of finite differences).These classical methods run into problems: symbolic differentiation leads to inefficient code (unless carefully done) and faces the difficulty of converting a computer program into a single expression, while numerical differentiation can introduce round-off errors in the discretization process and cancellation. Both classical methods have problems with calculating higher derivatives, where the complexity and errors increase. Finally, both classical methods are slow at computing the partial derivatives of a function with respect to many inputs, as is needed for gradient-based optimization algorithms. Automatic differentiation solves all of these problems.