MTH 131 syllabus
... cost, marginal revenue, and marginal profit at different levels of production ...
... cost, marginal revenue, and marginal profit at different levels of production ...
Relational Calculus
... query in DRC / TRC; the converse is also true. Relational Completeness: Query language (e.g., SQL) can express every query that is expressible in relational algebra/calculus. ...
... query in DRC / TRC; the converse is also true. Relational Completeness: Query language (e.g., SQL) can express every query that is expressible in relational algebra/calculus. ...
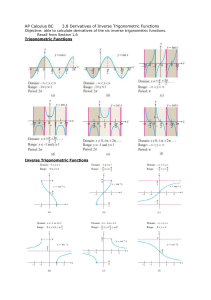
Trigonometry Test 7 Solve. Draw the diagram and show the work. (4
... Convert from degrees to radians and simplify. ...
... Convert from degrees to radians and simplify. ...
Lecture 7: Stochastic integrals and stochastic differential equations Eric Vanden-Eijnden
... (ρ(x, t|y) does not depends on s because b(x) and σ(x) are time-independent.) The transition probability density is an essential object because the process Xt is Markov, in other words: for any t, s ≥ 0 P(Xt+s ∈ B[x1 , x2 )|{Xs′ }0≤s′ ≤s }) = P(Xt+s ∈ B[x1 , x2 )|{Xs }), i.e.the future behavior of X ...
... (ρ(x, t|y) does not depends on s because b(x) and σ(x) are time-independent.) The transition probability density is an essential object because the process Xt is Markov, in other words: for any t, s ≥ 0 P(Xt+s ∈ B[x1 , x2 )|{Xs′ }0≤s′ ≤s }) = P(Xt+s ∈ B[x1 , x2 )|{Xs }), i.e.the future behavior of X ...
AP Physics (Review)
... The “dx” comes from the differential operator I “multiply” both sides by “dx” The quantity d(f(x)) represents a finite ...
... The “dx” comes from the differential operator I “multiply” both sides by “dx” The quantity d(f(x)) represents a finite ...
CHAPTER SIX: APPLICATIONS OF THE INTEGRAL
... fail to honor the vertical line test (the test that determines if a relation is actually a function). But these functions, on the hand, seem simpler if they were in terms of y. ...
... fail to honor the vertical line test (the test that determines if a relation is actually a function). But these functions, on the hand, seem simpler if they were in terms of y. ...
PowerPoint Presentation - KCPE-KCSE
... 1. Write the formulas for the cation and anion, including CHARGES! 2. Check to see if charges are balanced. 3. Balance charges , if necessary, ...
... 1. Write the formulas for the cation and anion, including CHARGES! 2. Check to see if charges are balanced. 3. Balance charges , if necessary, ...
ppt - marric.us
... 1. Write the formulas for the cation and anion, including CHARGES! 2. Check to see if charges are balanced. 3. Balance charges , if necessary, ...
... 1. Write the formulas for the cation and anion, including CHARGES! 2. Check to see if charges are balanced. 3. Balance charges , if necessary, ...
x2 +y2 = 25. We know the graph of this to be a
... So there are really functions sitting inside relationships even though we have not (or can not) solve those relationships for y in terms of x. We call functions of this type implicit functions, and this chapter discusses derivatives of such functions. The process of finding ...
... So there are really functions sitting inside relationships even though we have not (or can not) solve those relationships for y in terms of x. We call functions of this type implicit functions, and this chapter discusses derivatives of such functions. The process of finding ...
Fundamental theorem of calculus part 2
... Intuitively, I read this as "Adding up all the changes from a to b is the same as getting the difference between a and b". Formally, you'll see f(x)=steps(x) and F(x)=Original(x) Why is this cool? The definite integral is a gritty mechanical computation, and the indefinite integral is a nice, clean ...
... Intuitively, I read this as "Adding up all the changes from a to b is the same as getting the difference between a and b". Formally, you'll see f(x)=steps(x) and F(x)=Original(x) Why is this cool? The definite integral is a gritty mechanical computation, and the indefinite integral is a nice, clean ...
Overview of Junior Cert Honours Maths Paper
... This will be the main geometry Question They will ask you to prove a theorem more than likely using congruent triangles. You may also be asked to construct a triangle or a parallelogram. Question 4: Geometry. It is likely that in this question the will ask you to prove one of the last 5 theorems. Qu ...
... This will be the main geometry Question They will ask you to prove a theorem more than likely using congruent triangles. You may also be asked to construct a triangle or a parallelogram. Question 4: Geometry. It is likely that in this question the will ask you to prove one of the last 5 theorems. Qu ...
Automatic differentiation

In mathematics and computer algebra, automatic differentiation (AD), also called algorithmic differentiation or computational differentiation, is a set of techniques to numerically evaluate the derivative of a function specified by a computer program. AD exploits the fact that every computer program, no matter how complicated, executes a sequence of elementary arithmetic operations (addition, subtraction, multiplication, division, etc.) and elementary functions (exp, log, sin, cos, etc.). By applying the chain rule repeatedly to these operations, derivatives of arbitrary order can be computed automatically, accurately to working precision, and using at most a small constant factor more arithmetic operations than the original program.Automatic differentiation is not: Symbolic differentiation, nor Numerical differentiation (the method of finite differences).These classical methods run into problems: symbolic differentiation leads to inefficient code (unless carefully done) and faces the difficulty of converting a computer program into a single expression, while numerical differentiation can introduce round-off errors in the discretization process and cancellation. Both classical methods have problems with calculating higher derivatives, where the complexity and errors increase. Finally, both classical methods are slow at computing the partial derivatives of a function with respect to many inputs, as is needed for gradient-based optimization algorithms. Automatic differentiation solves all of these problems.