Homework - BetsyMcCall.net
... a. If f is a function in the vector space V of all real-valued functions on R and if f (t ) 0 for some t, then f is the zero vector in V. b. A vector is an arrow in three-dimensional space. c. A subset H of a vector space V is a subspace of V if the zero vector is in H. d. A subspace is also a vec ...
... a. If f is a function in the vector space V of all real-valued functions on R and if f (t ) 0 for some t, then f is the zero vector in V. b. A vector is an arrow in three-dimensional space. c. A subset H of a vector space V is a subspace of V if the zero vector is in H. d. A subspace is also a vec ...
Linear Independence
... 1.7: Linear Independence We will study homogeneous equations from a different perspective by writing them as vector equations. ...
... 1.7: Linear Independence We will study homogeneous equations from a different perspective by writing them as vector equations. ...
Solution Set - Harvard Math Department
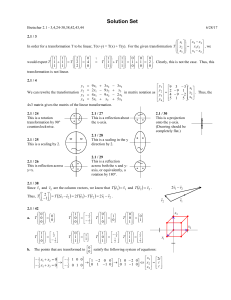
... In proving the above two conditions, we have used a few properties of cross product. Since both conditions are satisfied, the cross product transformation is linear. Using the definition of cross product, we can write: v x v x 0 v3 v2 x1 v x ...
... In proving the above two conditions, we have used a few properties of cross product. Since both conditions are satisfied, the cross product transformation is linear. Using the definition of cross product, we can write: v x v x 0 v3 v2 x1 v x ...



















![[2011 question paper]](http://s1.studyres.com/store/data/008881811_1-8ef23f7493d56bc511a2c01dcc81fc96-300x300.png)