Physics PHYS 354 Electricity and Magnetism II Problem Set #4
... The three unit vectors êi (i=1, 2, 3), as well as the êi , satisfy the relations ...
... The three unit vectors êi (i=1, 2, 3), as well as the êi , satisfy the relations ...
ECE 3300 Portfolio 1..
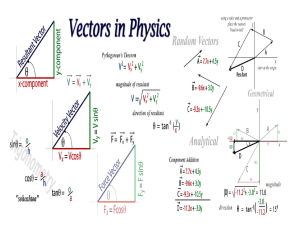
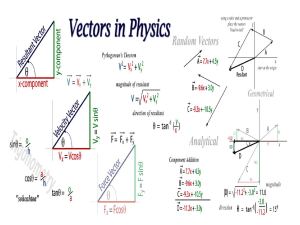
... we have an equation for E , it will be a vector that acts a s a function of x, y and z or whatever coordinate system applies. As we “plug-in” different values of x, y, and z, a vector with a specific angle and magnitude will result. Multiple points will form a “sketch” of fields comprised of vector ...
... we have an equation for E , it will be a vector that acts a s a function of x, y and z or whatever coordinate system applies. As we “plug-in” different values of x, y, and z, a vector with a specific angle and magnitude will result. Multiple points will form a “sketch” of fields comprised of vector ...
Matrices - University of Sunderland
... • A nonunit stride or step is denoted i:s:j. • Matrix subscripts (1 or greater!) are accessed as A(i,j). • A(p:q,r:s) is a submatrix of A. • A(:,j) is the jth column and A(i,:) is the ith row. • end represents the last column or row. ...
... • A nonunit stride or step is denoted i:s:j. • Matrix subscripts (1 or greater!) are accessed as A(i,j). • A(p:q,r:s) is a submatrix of A. • A(:,j) is the jth column and A(i,:) is the ith row. • end represents the last column or row. ...
Matrix Operations (10/6/04)
... Matrices can be added, scalar multiplied, and multiplied. The former two are simple; the last more complicated. A scalar t times a matrix A is just t times every entry of A. A + B means add all pairs of corresponding entries. A and B can only be added if they are the same size (both m by n, say). ...
... Matrices can be added, scalar multiplied, and multiplied. The former two are simple; the last more complicated. A scalar t times a matrix A is just t times every entry of A. A + B means add all pairs of corresponding entries. A and B can only be added if they are the same size (both m by n, say). ...
USE OF LINEAR ALGEBRA I Math 21b, O. Knill
... that a system can be in three different states a, b, c and that transitions a 7→ b, b 7→ a, b 7→ c, c 7→ c, c 7→ a are allowed. A possible evolution of the system is then a, b, a, b, a, c, c, c, a, b, c, a... One calls this a description of the system with symbolic dynamics. This language is used in ...
... that a system can be in three different states a, b, c and that transitions a 7→ b, b 7→ a, b 7→ c, c 7→ c, c 7→ a are allowed. A possible evolution of the system is then a, b, a, b, a, c, c, c, a, b, c, a... One calls this a description of the system with symbolic dynamics. This language is used in ...
Feature Generation
... • Φ must be invertible or of full column rank. • Identifiability condition: All independent components, y(i), must be non-Gaussian. Thus, in contrast to PCA that can always be performed, ICA is meaningful for non-Gaussian variables. • Under the above assumptions, y(i)’s can be uniquely estimated, wi ...
... • Φ must be invertible or of full column rank. • Identifiability condition: All independent components, y(i), must be non-Gaussian. Thus, in contrast to PCA that can always be performed, ICA is meaningful for non-Gaussian variables. • Under the above assumptions, y(i)’s can be uniquely estimated, wi ...