Quantum Mechanics II, Ex 4730
... Submitted by: Roee Steiner 034744821 Given a spherical shell with radius R and a particle with mass M and charge e. Notice that the standard variables which show the particle are (θ, φ, Lx, Ly, Lz) In this question we have to assume that the particle can be excited from ground state to first energy ...
... Submitted by: Roee Steiner 034744821 Given a spherical shell with radius R and a particle with mass M and charge e. Notice that the standard variables which show the particle are (θ, φ, Lx, Ly, Lz) In this question we have to assume that the particle can be excited from ground state to first energy ...
1 Polarization of Light
... The most general polarization state is |Φi = λ|xi+µ|yi where λ and µ are in general complex with |λ|2 + |µ|2 = 1. Then |Φi is normalized. In the case of linear polarization λ and µ are real and can be written as cos θ and sin θ. The basis states, |xi and |yi, form an orthonormal basis. The state of ...
... The most general polarization state is |Φi = λ|xi+µ|yi where λ and µ are in general complex with |λ|2 + |µ|2 = 1. Then |Φi is normalized. In the case of linear polarization λ and µ are real and can be written as cos θ and sin θ. The basis states, |xi and |yi, form an orthonormal basis. The state of ...
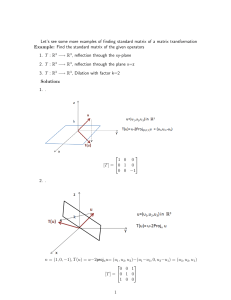
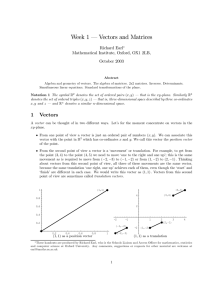
Week 1 – Vectors and Matrices
... • From one point of view a vector is just an ordered pair of numbers (x, y). We can associate this vector with the point in R2 which has co-ordinates x and y. We call this vector the position vector of the point. • From the second point of view a vector is a ‘movement’ or translation. For example, t ...
... • From one point of view a vector is just an ordered pair of numbers (x, y). We can associate this vector with the point in R2 which has co-ordinates x and y. We call this vector the position vector of the point. • From the second point of view a vector is a ‘movement’ or translation. For example, t ...