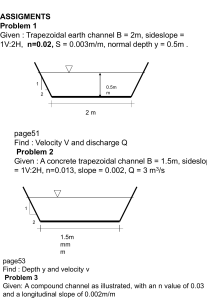
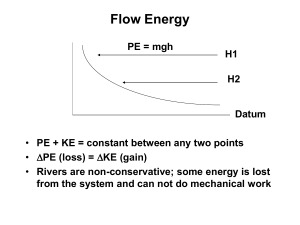
Fluid Mechanics Primer
... Because a fluid cannot resist deformation force, it moves, or flows under the action of the force. Its shape will change continuously as long as the force is applied. A solid can resist a deformation force while at rest. While a force may cause some displacement, the solid does not move indefinitely ...
... Because a fluid cannot resist deformation force, it moves, or flows under the action of the force. Its shape will change continuously as long as the force is applied. A solid can resist a deformation force while at rest. While a force may cause some displacement, the solid does not move indefinitely ...
Key Points on Chapter 15: Fluid Mechanics • Pressure is force per
... volume 12 ρv 2 , and the gravitational potential energy per unit volume ρgy has the same value at all points along a streamline. This means that if one terms increases, the other terms must decrease to compensate and keep the sum of terms constant. When the fluid is at rest, v1 = v2 = 0 and Bernoull ...
... volume 12 ρv 2 , and the gravitational potential energy per unit volume ρgy has the same value at all points along a streamline. This means that if one terms increases, the other terms must decrease to compensate and keep the sum of terms constant. When the fluid is at rest, v1 = v2 = 0 and Bernoull ...
Timothy J. Pedley
... drastically change their shape. This is the subject of collapsible tubes which I worked on for a long time. In the circumstances when a fairly thin-walled elastic tube is collapsing, you do not need much pressure change to create a relatively significant change in cross-sectional area and therefore ...
... drastically change their shape. This is the subject of collapsible tubes which I worked on for a long time. In the circumstances when a fairly thin-walled elastic tube is collapsing, you do not need much pressure change to create a relatively significant change in cross-sectional area and therefore ...
Bernoulli's principle

In fluid dynamics, Bernoulli's principle states that for an inviscid flow of a non-conducting fluid, an increase in the speed of the fluid occurs simultaneously with a decrease in pressure or a decrease in the fluid's potential energy. The principle is named after Daniel Bernoulli who published it in his book Hydrodynamica in 1738.Bernoulli's principle can be applied to various types of fluid flow, resulting in what is loosely denoted as Bernoulli's equation. In fact, there are different forms of the Bernoulli equation for different types of flow. The simple form of Bernoulli's principle is valid for incompressible flows (e.g. most liquid flows and gases moving at low Mach number). More advanced forms may in some cases be applied to compressible flows at higher Mach numbers (see the derivations of the Bernoulli equation). Bernoulli's principle can be derived from the principle of conservation of energy. This states that, in a steady flow, the sum of all forms of energy in a fluid along a streamline is the same at all points on that streamline. This requires that the sum of kinetic energy, potential energy and internal energy remains constant. Thus an increase in the speed of the fluid – implying an increase in both its dynamic pressure and kinetic energy – occurs with a simultaneous decrease in (the sum of) its static pressure, potential energy and internal energy. If the fluid is flowing out of a reservoir, the sum of all forms of energy is the same on all streamlines because in a reservoir the energy per unit volume (the sum of pressure and gravitational potential ρ g h) is the same everywhere.Bernoulli's principle can also be derived directly from Newton's 2nd law. If a small volume of fluid is flowing horizontally from a region of high pressure to a region of low pressure, then there is more pressure behind than in front. This gives a net force on the volume, accelerating it along the streamline.Fluid particles are subject only to pressure and their own weight. If a fluid is flowing horizontally and along a section of a streamline, where the speed increases it can only be because the fluid on that section has moved from a region of higher pressure to a region of lower pressure; and if its speed decreases, it can only be because it has moved from a region of lower pressure to a region of higher pressure. Consequently, within a fluid flowing horizontally, the highest speed occurs where the pressure is lowest, and the lowest speed occurs where the pressure is highest.