Full text
... If T1 is “breakable” at cell k − 1, which can happen fk−1 fn−k ways, then we have found a tiling of length k − 1. We would then look for a tiling of length k − 2, starting with tiling T2 . Otherwise, T1 is breakable at cell k − 2, followed by a domino (which happens fk−2 fn−k−1 ways. Here, we “throw ...
... If T1 is “breakable” at cell k − 1, which can happen fk−1 fn−k ways, then we have found a tiling of length k − 1. We would then look for a tiling of length k − 2, starting with tiling T2 . Otherwise, T1 is breakable at cell k − 2, followed by a domino (which happens fk−2 fn−k−1 ways. Here, we “throw ...
Overview for Year 2
... recall and use addition and subtraction facts to 20 fluently, and derive and use related facts up to 100 add and subtract numbers using concrete objects, pictorial representations, and mentally, including: – a two-digit number and ones – a two-digit number and tens – adding three one-digit numbe ...
... recall and use addition and subtraction facts to 20 fluently, and derive and use related facts up to 100 add and subtract numbers using concrete objects, pictorial representations, and mentally, including: – a two-digit number and ones – a two-digit number and tens – adding three one-digit numbe ...
Grade Seven Mathematics
... problems involving rates such as motion at a constant speed. GLE 0706.4.3 Understand and use scale factor to describe the relationships between length, area, and volume. GLE 0706.4.4 Understand and use ratios, derived quantities, and indirect measurements. Checks for Understanding (Formative/Summati ...
... problems involving rates such as motion at a constant speed. GLE 0706.4.3 Understand and use scale factor to describe the relationships between length, area, and volume. GLE 0706.4.4 Understand and use ratios, derived quantities, and indirect measurements. Checks for Understanding (Formative/Summati ...
10-4-10 - NISPLAN
... In 2003 the State Pension was increased by 2% to £78.03. What was the State Pension before this increase? This is quite a difficult percentage question! 100% represents the total state pension before the increase. We know that 100% + 2% increase = 102% = £78.03 Use the diagram to calculate 100%, by ...
... In 2003 the State Pension was increased by 2% to £78.03. What was the State Pension before this increase? This is quite a difficult percentage question! 100% represents the total state pension before the increase. We know that 100% + 2% increase = 102% = £78.03 Use the diagram to calculate 100%, by ...
Phi: That Golden Number
... Leonardo Fibonacci began study of this sequence by posing the following problem in his book, Liber Abaci How many pairs of rabbits will be produced in a year, beginning with a single pair, if in every month each pair bears a new pair, which becomes productive from the second month on? Of course, thi ...
... Leonardo Fibonacci began study of this sequence by posing the following problem in his book, Liber Abaci How many pairs of rabbits will be produced in a year, beginning with a single pair, if in every month each pair bears a new pair, which becomes productive from the second month on? Of course, thi ...
Aalborg Universitet Aesthetics and quality of numbers using the primety measure
... prime numbers, only brute force methods are guaranteed to render a result as to whether a number is prime or not. Many mathematicians will find the mathematics involved in prime numbers beautiful, or even artistic in its own right. Byers (2007) states: “Mathematics, as I have been describing it, is ...
... prime numbers, only brute force methods are guaranteed to render a result as to whether a number is prime or not. Many mathematicians will find the mathematics involved in prime numbers beautiful, or even artistic in its own right. Byers (2007) states: “Mathematics, as I have been describing it, is ...
basic counting
... • Once again we count by starting with all permutations of [n] and then using inclusion/exclusion to delete the permutations with fixed points. Let S be the set of permutations of [n]. That is, S={f:[n]→[n]} such that f is bijective. Further, for i=1,2,…,n, let Ai be the set of permutations of [n] t ...
... • Once again we count by starting with all permutations of [n] and then using inclusion/exclusion to delete the permutations with fixed points. Let S be the set of permutations of [n]. That is, S={f:[n]→[n]} such that f is bijective. Further, for i=1,2,…,n, let Ai be the set of permutations of [n] t ...
geometric sequences - Biblical Christian World View
... Technically, the sum of an infinite series converges to a finite number as a limit. The … (ad infinitum) tells you that the series continues “without end.” ...
... Technically, the sum of an infinite series converges to a finite number as a limit. The … (ad infinitum) tells you that the series continues “without end.” ...
- Ministry of Education, Guyana
... Schools Bk 1 Mathematics for Sec School in Guyana Bk 1 A Compl. Mths. Crse for Sec Schools Bk 1 Mathematics for Sec School in Guyana Bk 1 A Compl. Mths. Crse for Sec Schools Bk 1 ...
... Schools Bk 1 Mathematics for Sec School in Guyana Bk 1 A Compl. Mths. Crse for Sec Schools Bk 1 Mathematics for Sec School in Guyana Bk 1 A Compl. Mths. Crse for Sec Schools Bk 1 ...
7th Grade 2007 Math with MTAS-III Information
... & Symbols from MTAS Draft Test Specifications (1-2 tasks) ...
... & Symbols from MTAS Draft Test Specifications (1-2 tasks) ...
Evaluating the exact infinitesimal values of area of Sierpinski`s
... because the traditional mathematics (both standard and non-standard versions of Analysis) can speak only about limit fractal objects and the required values tend to zero or infinity. Let us consider, for example, the famous Cantor’s set (see Fig. 1). If a finite number of steps, n, has been done in ...
... because the traditional mathematics (both standard and non-standard versions of Analysis) can speak only about limit fractal objects and the required values tend to zero or infinity. Let us consider, for example, the famous Cantor’s set (see Fig. 1). If a finite number of steps, n, has been done in ...
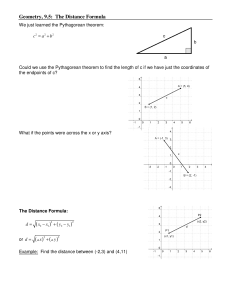
Geometry, 9.5: The Distance Formula
... Procedure for using Pythagorean triples to find a missing side: 1) Find a number that divides evenly into the 2 sides given. 2) Divide both sides by that number and write new side lengths in parentheses. 3) Match new sides to a Pythagorean triple and fill in missing side. 4) Make a proportion with t ...
... Procedure for using Pythagorean triples to find a missing side: 1) Find a number that divides evenly into the 2 sides given. 2) Divide both sides by that number and write new side lengths in parentheses. 3) Match new sides to a Pythagorean triple and fill in missing side. 4) Make a proportion with t ...
the golden ratio and the fibonacci sequence
... • Example. Golden Rectangle: Form a rectangle such that when the rectangle is divided into a square and another rectangle, the smaller rectangle is similar (proportional) to the original rectangle. What is the ratio of the length to the width? ...
... • Example. Golden Rectangle: Form a rectangle such that when the rectangle is divided into a square and another rectangle, the smaller rectangle is similar (proportional) to the original rectangle. What is the ratio of the length to the width? ...
7.1 Ratios and Proportions - William H. Peacock, LCDR USN
... class and found that 18 had a dog or a cat for a pet. If there are 870 students in Monique’s school, predict the total number of students with a dog or a cat. Write and solve a proportion that compares the number of students who have a pet to the number of students in the ...
... class and found that 18 had a dog or a cat for a pet. If there are 870 students in Monique’s school, predict the total number of students with a dog or a cat. Write and solve a proportion that compares the number of students who have a pet to the number of students in the ...
DO NOW (not later):
... Step 1 – Write the ratio as a fraction Step 2 – Simplify the fraction (Find the greatest common factor (GCF) of both numbers and divide the numerator and denominator by the GCF). Step 3 – Write the equivalent ratio in the same form as the question ...
... Step 1 – Write the ratio as a fraction Step 2 – Simplify the fraction (Find the greatest common factor (GCF) of both numbers and divide the numerator and denominator by the GCF). Step 3 – Write the equivalent ratio in the same form as the question ...
DO NOW (not later) - World of Teaching
... Step 1 – Write the ratio as a fraction Step 2 – Simplify the fraction (Find the greatest common factor (GCF) of both numbers and divide the numerator and denominator by the GCF). Step 3 – Write the equivalent ratio in the same form as the question ...
... Step 1 – Write the ratio as a fraction Step 2 – Simplify the fraction (Find the greatest common factor (GCF) of both numbers and divide the numerator and denominator by the GCF). Step 3 – Write the equivalent ratio in the same form as the question ...
EE Pacing Guide - essentialelementsutah
... probability of events occurring as possible or impossible. (7th) C4.2 I can graph a simple ratio by connecting the origin to a point representing the ratio in the form of y/x. (8th) C3.2 I can answer questions, compare sets of data. (7th) C4.2 I can identify a missing number that completes another o ...
... probability of events occurring as possible or impossible. (7th) C4.2 I can graph a simple ratio by connecting the origin to a point representing the ratio in the form of y/x. (8th) C3.2 I can answer questions, compare sets of data. (7th) C4.2 I can identify a missing number that completes another o ...
Figurate Numbers
... Some species include: 1. Lilies, irises and clover have 3 petals. 2. Buttercups and some delphiniums have 5 petals. 3. Other kinds of delphiniums have 8 petals. ...
... Some species include: 1. Lilies, irises and clover have 3 petals. 2. Buttercups and some delphiniums have 5 petals. 3. Other kinds of delphiniums have 8 petals. ...
Open Day Presentation
... – questions are hard compared to A level – there is a commonality of style ...
... – questions are hard compared to A level – there is a commonality of style ...
Mathematics and art

Mathematics and art are related in a variety of ways. Mathematics has itself been described as an art motivated by beauty. Mathematics can be discerned in arts such as music, dance, painting, architecture, sculpture, and textiles. This article focuses, however, on mathematics in the visual arts.Mathematics and art have a long historical relationship. Artists have used mathematics since the 5th century BC when the Greek sculptor Polykleitos wrote his Canon, prescribing proportions based on the ratio 1:√2 for the ideal male nude. Persistent popular claims have been made for the use of the golden ratio in ancient times, without reliable evidence. In the Italian Renaissance, Luca Pacioli wrote the influential treatise De Divina Proportione (1509), illustrated with woodcuts by Leonardo da Vinci, on the use of proportion in art. Another Italian painter, Piero della Francesca, developed Euclid's ideas on perspective in treatises such as De Prospectiva Pingendi, and in his paintings. The engraver Albrecht Dürer made many references to mathematics in his work Melencolia I. In modern times, the graphic artist M. C. Escher made intensive use of tessellation and hyperbolic geometry, with the help of the mathematician H. S. M. Coxeter, while the De Stijl movement led by Theo van Doesberg and Piet Mondrian explicitly embraced geometrical forms. Mathematics has inspired textile arts such as quilting, knitting, cross-stitch, crochet, embroidery, weaving, Turkish and other carpet-making, as well as kilim.Mathematics has directly influenced art with conceptual tools such as linear perspective, the analysis of symmetry and mathematical objects such as polyhedra and the Möbius strip. The construction of models of mathematical objects for research or teaching has led repeatedly to artwork, sometimes by mathematicians such as Magnus Wenninger who creates colourful stellated polyhedra. Mathematical concepts such as recursion and logical paradox can be seen in paintings by Rene Magritte, in engravings by M. C. Escher, and in computer art which often makes use of fractals, cellular automata and the Mandelbrot set. Controversially, the artist David Hockney has argued that artists from the Renaissance onwards made use of the camera lucida to draw precise representations of scenes; the architect Philip Steadman similarly argued that Vermeer used the camera obscura in his distinctively observed paintings.Other relationships include the algorithimic analysis of artworks by X-ray fluorescence spectroscopy; the stimulus to mathematics research by Filippo Brunelleschi's theory of perspective which eventually led to Girard Desargues's projective geometry; and the persistent view, based ultimately on the Pythagorean notion of harmony in music and the view that everything was arranged by Number, that God is the geometer of the world, and that the world's geometry is therefore sacred. This is seen in artworks such as William Blake's The Ancient of Days.