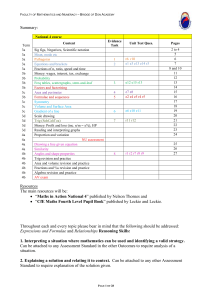
Mathematics Guidelines for Practical: English Medium
... It is a general saying that mathematics is by doing only. The concepts for which the proof/verification is done by experimentation or activities are better understood by learners are retained in their brains for longer period of time. Jen Piaget, an psychologists, while writing his thesis on concept ...
... It is a general saying that mathematics is by doing only. The concepts for which the proof/verification is done by experimentation or activities are better understood by learners are retained in their brains for longer period of time. Jen Piaget, an psychologists, while writing his thesis on concept ...
Running Time of Euclidean Algorithm
... Base case: If n = 1, then there is only one line and therefore no intersections. On the other hand, plugging n = 1 into n(n-1)/2 gives 0, so the base case holds. ...
... Base case: If n = 1, then there is only one line and therefore no intersections. On the other hand, plugging n = 1 into n(n-1)/2 gives 0, so the base case holds. ...
tasks - Georgia Mathematics Educator Forum
... Rewrite (simplify) expressions involving radicals. Use and explain properties of rational and irrational numbers. Explain why the sum or product of rational numbers is rational; why the sum of a rational number and an irrational number is irrational; and why the product of a nonzero rational n ...
... Rewrite (simplify) expressions involving radicals. Use and explain properties of rational and irrational numbers. Explain why the sum or product of rational numbers is rational; why the sum of a rational number and an irrational number is irrational; and why the product of a nonzero rational n ...
Pythagoras and the Pythagoreans
... • A prime number is rectilinear, meaning that it can only be set out in one dimension. The number 2 was not originally regarded as a prime number, or even as a number at all. • A composite number is that which is measured by (has a factor) some number. (Euclid) • Two numbers are prime to one another ...
... • A prime number is rectilinear, meaning that it can only be set out in one dimension. The number 2 was not originally regarded as a prime number, or even as a number at all. • A composite number is that which is measured by (has a factor) some number. (Euclid) • Two numbers are prime to one another ...
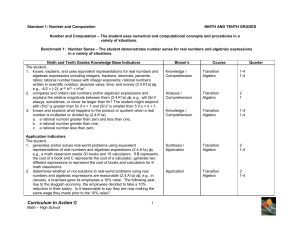
Unit B391/01 – Sample scheme of work and lesson plan
... produced sample schemes of work and lesson plans for Methods in Mathematics. These support materials are designed for guidance only and play a secondary role to the specification. Each scheme of work and lesson plan is provided in Word format – so that you can use it as a foundation to build upon an ...
... produced sample schemes of work and lesson plans for Methods in Mathematics. These support materials are designed for guidance only and play a secondary role to the specification. Each scheme of work and lesson plan is provided in Word format – so that you can use it as a foundation to build upon an ...
Lesson 1.3 Exercises, pages 35–42
... For each sequence, I wrote an equation for the 5th term, then solved the equation to determine the common difference and common ratio. For the arithmetic sequence, I added the common difference to get the next terms. For the geometric sequences, there were two possible common ratios, and I multiplie ...
... For each sequence, I wrote an equation for the 5th term, then solved the equation to determine the common difference and common ratio. For the arithmetic sequence, I added the common difference to get the next terms. For the geometric sequences, there were two possible common ratios, and I multiplie ...
ppt - School of Computer Science
... Church and Turing were both interested in the number of whorls in each ring of the spiral. The ratio of consecutive ring lengths approaches the Golden Ratio. ...
... Church and Turing were both interested in the number of whorls in each ring of the spiral. The ratio of consecutive ring lengths approaches the Golden Ratio. ...
SUPPORT - Pearson Schools and FE Colleges
... subsequent units of a topic need careful adjusting in the light of teachers’ assessment of pupils’ progress); How objectives for using and applying mathematics can be incorporated into units. For each term, suggested objectives for oral and mental mathematics are also identified. Oral and mental w ...
... subsequent units of a topic need careful adjusting in the light of teachers’ assessment of pupils’ progress); How objectives for using and applying mathematics can be incorporated into units. For each term, suggested objectives for oral and mental mathematics are also identified. Oral and mental w ...
Grade 6 Mathematics Assessment Anchors and Eligible Content
... of a ratio relationship. Example 1: “This recipe has a ratio of 3 cups of flour to 4 cups of sugar, so there is 3/4 cup of flour for each cup of sugar.” Example 2: “We paid $75 for 15 hamburgers, which is a rate of $5 per hamburger.” Construct tables of equivalent ratios relating quantities with who ...
... of a ratio relationship. Example 1: “This recipe has a ratio of 3 cups of flour to 4 cups of sugar, so there is 3/4 cup of flour for each cup of sugar.” Example 2: “We paid $75 for 15 hamburgers, which is a rate of $5 per hamburger.” Construct tables of equivalent ratios relating quantities with who ...
Pythagorean Triples Solution Commentary:
... Extension Problem #2 explored Euclid’s method for producing Pythagorean triples. This method has been analyzed and discussed often as to whether or not Euclid’s method produces all of the triples. Laubenbacher & Pengelley (1999 pp. 172-178) document thoroughly that this is the case, though such may ...
... Extension Problem #2 explored Euclid’s method for producing Pythagorean triples. This method has been analyzed and discussed often as to whether or not Euclid’s method produces all of the triples. Laubenbacher & Pengelley (1999 pp. 172-178) document thoroughly that this is the case, though such may ...
Standard Grade - Maths4Scotland
... What are Surds A surd is an irrational number An irrational number cannot be written as a simple fraction i.e. as ...
... What are Surds A surd is an irrational number An irrational number cannot be written as a simple fraction i.e. as ...
Geometry of Flat Surfaces
... Let 2d be the number of sides of the polygon. Apparently, for d = 2 we have ν2 = 0 for d = 3 we have ν2 = 0 for d = 4 we have ν2 = 1/3 for d = 5 we have ν2 = 1/2 (all rational...) for d = 6 we have ν2 = 0, 6156 . . . or 0, 7173 . . . (probably irrational...) Conjecture (Kontsevich-Zorich). The sum ν ...
... Let 2d be the number of sides of the polygon. Apparently, for d = 2 we have ν2 = 0 for d = 3 we have ν2 = 0 for d = 4 we have ν2 = 1/3 for d = 5 we have ν2 = 1/2 (all rational...) for d = 6 we have ν2 = 0, 6156 . . . or 0, 7173 . . . (probably irrational...) Conjecture (Kontsevich-Zorich). The sum ν ...
Keynote: Structure and Coherence: Telling the Story of the Journey
... 3Grade3ThemeaningoffractionsInGrades1and2,studentsusefractionlanguagetodescribepartitionsofshapesintoequalshares.2.G.3In2.G.3Partitioncirclesandrectanglesintotwo,three,orfourequalshares,describethesharesusingthewordshalves,thirds,halfof,athirdof,etc.,anddescribethewholeastwohalves,threethirds,fourfo ...
... 3Grade3ThemeaningoffractionsInGrades1and2,studentsusefractionlanguagetodescribepartitionsofshapesintoequalshares.2.G.3In2.G.3Partitioncirclesandrectanglesintotwo,three,orfourequalshares,describethesharesusingthewordshalves,thirds,halfof,athirdof,etc.,anddescribethewholeastwohalves,threethirds,fourfo ...
Read full issue - Canadian Mathematical Society
... 4. ABCD is a square. Three parallel lines l1 , l2 and l3 pass through A, B and C respectively. The distance between l1 and l2 is 5 and the distance between l2 and l3 is 7. Find the area of ABCD. 5. The sum of the lengths of the three sides of a right triangle is 18. The sum of the squares of the len ...
... 4. ABCD is a square. Three parallel lines l1 , l2 and l3 pass through A, B and C respectively. The distance between l1 and l2 is 5 and the distance between l2 and l3 is 7. Find the area of ABCD. 5. The sum of the lengths of the three sides of a right triangle is 18. The sum of the squares of the len ...
in solving problems
... Make sure that you have a copy of the Formulae and Tables Booklet. You should answer ALL the questions in this booklet. Show ALL working for ALL questions. Show any derivative(s) that you need to find when solving the problems. The questions in this booklet are NOT in order of difficulty. Attempt al ...
... Make sure that you have a copy of the Formulae and Tables Booklet. You should answer ALL the questions in this booklet. Show ALL working for ALL questions. Show any derivative(s) that you need to find when solving the problems. The questions in this booklet are NOT in order of difficulty. Attempt al ...
Mathematics Embedded in Akan Weaving Patterns
... by the appropriate rituals and where taboos are observed. So the Akan have their “Divine drums” and the loom can be called “Kofi, the Creator's loom”. According to the Asante, during the reign of Oti Akenten, an Asante chief from an earlier period, one Ota Kraban journeyed to Gyaman (in present day ...
... by the appropriate rituals and where taboos are observed. So the Akan have their “Divine drums” and the loom can be called “Kofi, the Creator's loom”. According to the Asante, during the reign of Oti Akenten, an Asante chief from an earlier period, one Ota Kraban journeyed to Gyaman (in present day ...
F6 Solving Inequalities Introduction
... A more recent application of solving sets of inequalities is that of linear programming. This technique was developed during the 2nd World War by the mathematicians, John von Neuman (1905–1957) and George Dantzig (1914–2005), in order to solve problems of optimising convoys across the Atlantic. Sinc ...
... A more recent application of solving sets of inequalities is that of linear programming. This technique was developed during the 2nd World War by the mathematicians, John von Neuman (1905–1957) and George Dantzig (1914–2005), in order to solve problems of optimising convoys across the Atlantic. Sinc ...
Mathematics and art

Mathematics and art are related in a variety of ways. Mathematics has itself been described as an art motivated by beauty. Mathematics can be discerned in arts such as music, dance, painting, architecture, sculpture, and textiles. This article focuses, however, on mathematics in the visual arts.Mathematics and art have a long historical relationship. Artists have used mathematics since the 5th century BC when the Greek sculptor Polykleitos wrote his Canon, prescribing proportions based on the ratio 1:√2 for the ideal male nude. Persistent popular claims have been made for the use of the golden ratio in ancient times, without reliable evidence. In the Italian Renaissance, Luca Pacioli wrote the influential treatise De Divina Proportione (1509), illustrated with woodcuts by Leonardo da Vinci, on the use of proportion in art. Another Italian painter, Piero della Francesca, developed Euclid's ideas on perspective in treatises such as De Prospectiva Pingendi, and in his paintings. The engraver Albrecht Dürer made many references to mathematics in his work Melencolia I. In modern times, the graphic artist M. C. Escher made intensive use of tessellation and hyperbolic geometry, with the help of the mathematician H. S. M. Coxeter, while the De Stijl movement led by Theo van Doesberg and Piet Mondrian explicitly embraced geometrical forms. Mathematics has inspired textile arts such as quilting, knitting, cross-stitch, crochet, embroidery, weaving, Turkish and other carpet-making, as well as kilim.Mathematics has directly influenced art with conceptual tools such as linear perspective, the analysis of symmetry and mathematical objects such as polyhedra and the Möbius strip. The construction of models of mathematical objects for research or teaching has led repeatedly to artwork, sometimes by mathematicians such as Magnus Wenninger who creates colourful stellated polyhedra. Mathematical concepts such as recursion and logical paradox can be seen in paintings by Rene Magritte, in engravings by M. C. Escher, and in computer art which often makes use of fractals, cellular automata and the Mandelbrot set. Controversially, the artist David Hockney has argued that artists from the Renaissance onwards made use of the camera lucida to draw precise representations of scenes; the architect Philip Steadman similarly argued that Vermeer used the camera obscura in his distinctively observed paintings.Other relationships include the algorithimic analysis of artworks by X-ray fluorescence spectroscopy; the stimulus to mathematics research by Filippo Brunelleschi's theory of perspective which eventually led to Girard Desargues's projective geometry; and the persistent view, based ultimately on the Pythagorean notion of harmony in music and the view that everything was arranged by Number, that God is the geometer of the world, and that the world's geometry is therefore sacred. This is seen in artworks such as William Blake's The Ancient of Days.