Ratio
... It is important that you compare things of the same kind. For example, length must be compared with length, not with weight. In comparing things we usually make sure that they are measured in the same units. ...
... It is important that you compare things of the same kind. For example, length must be compared with length, not with weight. In comparing things we usually make sure that they are measured in the same units. ...
2: Multiplication can Increase or Decrease a Number
... Owing is the opposite of having, so we find that we can associate the concept of 'minus' with '(the) opposite (of)'. This also works in reverse. Thus, ( −4) × 8 means "owing £4, eight times over" or "owing £32" which is −£32 . Now −32 is smaller than 8, so we have illustrated another case where mult ...
... Owing is the opposite of having, so we find that we can associate the concept of 'minus' with '(the) opposite (of)'. This also works in reverse. Thus, ( −4) × 8 means "owing £4, eight times over" or "owing £32" which is −£32 . Now −32 is smaller than 8, so we have illustrated another case where mult ...
MT March 2016 Examination Paper – Final
... A box contains 6 green paperclips and 4 blue paperclips. Two paperclips are selected at random without replacement. i) ...
... A box contains 6 green paperclips and 4 blue paperclips. Two paperclips are selected at random without replacement. i) ...
Math Message and Number Sequences
... skills encountered earlier. The lessons are designed to build on concepts and skills throughout the year instead of treating them as isolated bits of knowledge. A curriculum that explores mathematical content beyond basic arithmetic Mathematics standards around the world indicate that basic arithmet ...
... skills encountered earlier. The lessons are designed to build on concepts and skills throughout the year instead of treating them as isolated bits of knowledge. A curriculum that explores mathematical content beyond basic arithmetic Mathematics standards around the world indicate that basic arithmet ...
End of Autumn term expectations for Maths – Year 2 Please note: by
... Please note: by the end of Year 2 your child is expected to tackle a range of mathematical challenges with enthusiasm and competently apply their mathematical skills to solve problems. Number ...
... Please note: by the end of Year 2 your child is expected to tackle a range of mathematical challenges with enthusiasm and competently apply their mathematical skills to solve problems. Number ...
Powerpoint
... 1. Make up an equation where the answer is x = 2 2. Make up an equation where the answer is x = 3 3. Make up an equation where …. Another idea: ...
... 1. Make up an equation where the answer is x = 2 2. Make up an equation where the answer is x = 3 3. Make up an equation where …. Another idea: ...
Name Period _____ Date 8.1 Ratios Ratio – Compares two
... = 1 : 4 = 1 to 4 (all of these ratios are said “one to four”) ...
... = 1 : 4 = 1 to 4 (all of these ratios are said “one to four”) ...
MPS Algebra/Geometry Syllabus Template
... classification levels were created in 2005 to analyze the depth of thinking a student is expected to demonstrate when completing an assessment. An overall depth of thinking must be associated with each benchmark in order to accurately interpret student achievement. It is important that analyzing th ...
... classification levels were created in 2005 to analyze the depth of thinking a student is expected to demonstrate when completing an assessment. An overall depth of thinking must be associated with each benchmark in order to accurately interpret student achievement. It is important that analyzing th ...
Fifth-Grade English Language Arts - Dorsey
... In Grade 5 Mathematics, students studied classification of counting numbers into subsets with distinguishing characteristics such as odd and even numbers and prime and composite numbers. Students also developed a strong foundation for understanding and applying multiples and factors. They will exten ...
... In Grade 5 Mathematics, students studied classification of counting numbers into subsets with distinguishing characteristics such as odd and even numbers and prime and composite numbers. Students also developed a strong foundation for understanding and applying multiples and factors. They will exten ...
MATHEMATICS
... c) Put the following in order, smallest first. Use 1 to represent the smallest amount and 4 to represent the largest amount of people watching the match. Number of men watching the match Number of boys watching the match Number of women watching the match Number of girls watching the match (6 marks) ...
... c) Put the following in order, smallest first. Use 1 to represent the smallest amount and 4 to represent the largest amount of people watching the match. Number of men watching the match Number of boys watching the match Number of women watching the match Number of girls watching the match (6 marks) ...
On Paracompactness of Metrizable Spaces
... Summary. The aim is to prove, using Mizar System, one of the most important result in general topology, namely the Stone Theorem on paracompactness of metrizable spaces [19]. Our proof is based on [18] (and also [16]). We prove first auxiliary fact that every open cover of any metrizable space has a ...
... Summary. The aim is to prove, using Mizar System, one of the most important result in general topology, namely the Stone Theorem on paracompactness of metrizable spaces [19]. Our proof is based on [18] (and also [16]). We prove first auxiliary fact that every open cover of any metrizable space has a ...
coursesyllabus7thgrade - Claiborne County Schools
... ● I can solve problems with scale drawings of geometric figures, compute actual lengths and area from a scale drawing, and reproduce a scale drawing using a different scale. ● I can draw (freehand, with ruler and protractor, with technology) geometric shapes with given conditions (focus on tria ...
... ● I can solve problems with scale drawings of geometric figures, compute actual lengths and area from a scale drawing, and reproduce a scale drawing using a different scale. ● I can draw (freehand, with ruler and protractor, with technology) geometric shapes with given conditions (focus on tria ...
Geometry CP Name: HR: ______
... rectangular fence for sunbathing. The shape of the pool is similar to the shape of the fence. The pool is 30 feet wide. The fence is 50 feet wide and 100 feet long. a) What is the scale factor of the pool to the fence? ...
... rectangular fence for sunbathing. The shape of the pool is similar to the shape of the fence. The pool is 30 feet wide. The fence is 50 feet wide and 100 feet long. a) What is the scale factor of the pool to the fence? ...
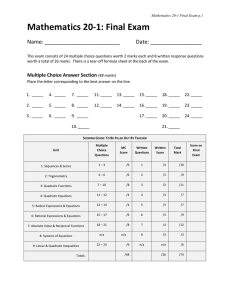
Mathematics 20-1 Final Exam Multiple Choice Questions
... Mathematics 20-1 Final Exam Multiple Choice Questions (2 marks each) Record your answers on the front cover of the exam. 1. What are the missing terms of the arithmetic sequence: __, 3, 9, __, __? a) 1, 27, 81 b) 9, 3, 9 c) -6, 12, 17 d) -3, 15, 21 ...
... Mathematics 20-1 Final Exam Multiple Choice Questions (2 marks each) Record your answers on the front cover of the exam. 1. What are the missing terms of the arithmetic sequence: __, 3, 9, __, __? a) 1, 27, 81 b) 9, 3, 9 c) -6, 12, 17 d) -3, 15, 21 ...
Toward greater focus and coherence
... device to expand a product such as (a + b)(x + y) and a student who can explain where the mnemonic comes from. The student who can explain the rule understands the mathematics, and may have a better chance to succeed at a less familiar task such as expanding (a + b + c)(x + y). Mathematical understa ...
... device to expand a product such as (a + b)(x + y) and a student who can explain where the mnemonic comes from. The student who can explain the rule understands the mathematics, and may have a better chance to succeed at a less familiar task such as expanding (a + b + c)(x + y). Mathematical understa ...
Mathematical Statements and Their Proofs
... Let a and b be two even integers. Since they are even, they can be written in the forms a = 2x and b = 2y for some integers x and y, respectively. Then, a + b can be written in the form 2x + 2y, giving the following equation: a + b = 2x + 2y = 2(x + y) From this, we see that a + b is divisible by 2. ...
... Let a and b be two even integers. Since they are even, they can be written in the forms a = 2x and b = 2y for some integers x and y, respectively. Then, a + b can be written in the form 2x + 2y, giving the following equation: a + b = 2x + 2y = 2(x + y) From this, we see that a + b is divisible by 2. ...
Mathematics and art

Mathematics and art are related in a variety of ways. Mathematics has itself been described as an art motivated by beauty. Mathematics can be discerned in arts such as music, dance, painting, architecture, sculpture, and textiles. This article focuses, however, on mathematics in the visual arts.Mathematics and art have a long historical relationship. Artists have used mathematics since the 5th century BC when the Greek sculptor Polykleitos wrote his Canon, prescribing proportions based on the ratio 1:√2 for the ideal male nude. Persistent popular claims have been made for the use of the golden ratio in ancient times, without reliable evidence. In the Italian Renaissance, Luca Pacioli wrote the influential treatise De Divina Proportione (1509), illustrated with woodcuts by Leonardo da Vinci, on the use of proportion in art. Another Italian painter, Piero della Francesca, developed Euclid's ideas on perspective in treatises such as De Prospectiva Pingendi, and in his paintings. The engraver Albrecht Dürer made many references to mathematics in his work Melencolia I. In modern times, the graphic artist M. C. Escher made intensive use of tessellation and hyperbolic geometry, with the help of the mathematician H. S. M. Coxeter, while the De Stijl movement led by Theo van Doesberg and Piet Mondrian explicitly embraced geometrical forms. Mathematics has inspired textile arts such as quilting, knitting, cross-stitch, crochet, embroidery, weaving, Turkish and other carpet-making, as well as kilim.Mathematics has directly influenced art with conceptual tools such as linear perspective, the analysis of symmetry and mathematical objects such as polyhedra and the Möbius strip. The construction of models of mathematical objects for research or teaching has led repeatedly to artwork, sometimes by mathematicians such as Magnus Wenninger who creates colourful stellated polyhedra. Mathematical concepts such as recursion and logical paradox can be seen in paintings by Rene Magritte, in engravings by M. C. Escher, and in computer art which often makes use of fractals, cellular automata and the Mandelbrot set. Controversially, the artist David Hockney has argued that artists from the Renaissance onwards made use of the camera lucida to draw precise representations of scenes; the architect Philip Steadman similarly argued that Vermeer used the camera obscura in his distinctively observed paintings.Other relationships include the algorithimic analysis of artworks by X-ray fluorescence spectroscopy; the stimulus to mathematics research by Filippo Brunelleschi's theory of perspective which eventually led to Girard Desargues's projective geometry; and the persistent view, based ultimately on the Pythagorean notion of harmony in music and the view that everything was arranged by Number, that God is the geometer of the world, and that the world's geometry is therefore sacred. This is seen in artworks such as William Blake's The Ancient of Days.