4) Write the similarity statement comparing the three triangles
... If we consider the proportion ax = xb you will notice that the means of the proportions are the same number. That number is the geometric mean of the extremes. Geometric Mean – given two numbers “a” and “b”, use the following formula to find the geometric mean “x”. ...
... If we consider the proportion ax = xb you will notice that the means of the proportions are the same number. That number is the geometric mean of the extremes. Geometric Mean – given two numbers “a” and “b”, use the following formula to find the geometric mean “x”. ...
Gr. 5 Math: Unit 2 - Algebra
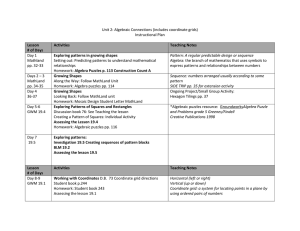
... Exploring patterns in growing shapes Setting out: Predicting patterns to understand mathematical relationships Homework: Algebra Puzzles p. 113 Construction Count A Growing Shapes Along the Way: Follow MathLand Unit Homework: Algebra puzzles pp. 114 Growing Shapes Looking Back: Follow MathLand unit ...
... Exploring patterns in growing shapes Setting out: Predicting patterns to understand mathematical relationships Homework: Algebra Puzzles p. 113 Construction Count A Growing Shapes Along the Way: Follow MathLand Unit Homework: Algebra puzzles pp. 114 Growing Shapes Looking Back: Follow MathLand unit ...
Fundamental Counting Principle (the multiplication principle)
... c) How many of these arrangements have all the N’s together? ...
... c) How many of these arrangements have all the N’s together? ...
math-gk-m2-topic-c
... (e.g., number of sides and vertices/”corners”) and other attributes (e.g., having sides of equal length). ...
... (e.g., number of sides and vertices/”corners”) and other attributes (e.g., having sides of equal length). ...
Summer 2013
... The diagram below (resource from NY multiple-subject sample question) could be used to model which of the following? A. B. C. D. ...
... The diagram below (resource from NY multiple-subject sample question) could be used to model which of the following? A. B. C. D. ...
Spreadsheet-Enhanced Problem Solving in Context as Modeling
... take intellectual risk through the formulation of mathematically meaningful questions about numerical patterns observed. In such an intellectual milieu the instructor’s ability to possess ‘the answer’ may not be an imperative [41], thus both parties could work as equal partners towards generating ne ...
... take intellectual risk through the formulation of mathematically meaningful questions about numerical patterns observed. In such an intellectual milieu the instructor’s ability to possess ‘the answer’ may not be an imperative [41], thus both parties could work as equal partners towards generating ne ...
Grade 7 Accelerated Math Scope and Sequence
... Reteaching/Enrichment: Week of November 18 – November 27 (+6 instructional days, 1 testing) ...
... Reteaching/Enrichment: Week of November 18 – November 27 (+6 instructional days, 1 testing) ...
DO NOW (not later):
... A bag contains 18 yellow, blue, and red marbles. The ratio of yellow to blue to red marbles is 4 : 2 : 3. ...
... A bag contains 18 yellow, blue, and red marbles. The ratio of yellow to blue to red marbles is 4 : 2 : 3. ...
Aalborg Universitet Numerical Investigation of the Primety of Real numbers
... mathematics involved in prime numbers beautiful, or even artistic in its own right. [2] states it Mathematics, as I have been describing it, is an art form. The words ambiguity and metaphor are much more acceptable in the arts than they are in the sciences. But ambiguity and metaphor are the mechani ...
... mathematics involved in prime numbers beautiful, or even artistic in its own right. [2] states it Mathematics, as I have been describing it, is an art form. The words ambiguity and metaphor are much more acceptable in the arts than they are in the sciences. But ambiguity and metaphor are the mechani ...
MEYL624 TUTOR NOTES Module 2
... Mathematical thinking is concerned with communicating, problem solving, logical reasoning, information processing, being creative, making connections, and selecting tools. There is no right answer to this task. The division of cards into the two groups will be subjective as it will depend on what yo ...
... Mathematical thinking is concerned with communicating, problem solving, logical reasoning, information processing, being creative, making connections, and selecting tools. There is no right answer to this task. The division of cards into the two groups will be subjective as it will depend on what yo ...
Family Letter
... Kindergarten mathematics is about: (1) representing, relating, and operating on whole numbers, initially with sets of objects; (2) describing shapes and space. More learning time in Kindergarten will be devoted to number than to other topics. The learning goal for each student is to achieve mastery ...
... Kindergarten mathematics is about: (1) representing, relating, and operating on whole numbers, initially with sets of objects; (2) describing shapes and space. More learning time in Kindergarten will be devoted to number than to other topics. The learning goal for each student is to achieve mastery ...
Equations - Translating, Writing, & Solving
... Step 1 Read the problem, several times if necessary, until you understand what is given and what is to be found. Step 2 If possible draw a picture or diagram to help visualize the problem. Step 3 Assign a variable to represent the unknown value, using diagrams or tables as needed. Write down what th ...
... Step 1 Read the problem, several times if necessary, until you understand what is given and what is to be found. Step 2 If possible draw a picture or diagram to help visualize the problem. Step 3 Assign a variable to represent the unknown value, using diagrams or tables as needed. Write down what th ...
Papick.pdf
... there exist a quadratic polynomial function whose graph passes through those points? Justify your answer. Raising this question certainly does not depend upon knowing the previous observation, but the classroom investigation connected to this question could be so much richer if a teacher were equipp ...
... there exist a quadratic polynomial function whose graph passes through those points? Justify your answer. Raising this question certainly does not depend upon knowing the previous observation, but the classroom investigation connected to this question could be so much richer if a teacher were equipp ...
Problems in relating various tasks and their sample solutions to
... (2) Comprehension, (3) Application, (4) Analysis, (5) Synthesis, and (6) Evaluation. This does not, however, make sense without examples demonstrating how such levels should be applied to the particular field under study, in this case mathematics. Applied to mathematics the first level (knowledge) c ...
... (2) Comprehension, (3) Application, (4) Analysis, (5) Synthesis, and (6) Evaluation. This does not, however, make sense without examples demonstrating how such levels should be applied to the particular field under study, in this case mathematics. Applied to mathematics the first level (knowledge) c ...
Exam 1 Study Guide MA 111 Spring 2015 It is suggested you review
... (22) Perform the following computations in S5 : (a) [1 2 3] [2 5 4] (b) [1 2] [2 3] [3 5] [5 4] (23) Let g = [1 2 3 4 5 6][7 8 9] in S9 . (a) Let t = [2 5]. Draw convincing pictures to show how the cycle number of g ◦ t differs from the cycle number of g. (b) Let t = [4 8]. Draw convincing pictures ...
... (22) Perform the following computations in S5 : (a) [1 2 3] [2 5 4] (b) [1 2] [2 3] [3 5] [5 4] (23) Let g = [1 2 3 4 5 6][7 8 9] in S9 . (a) Let t = [2 5]. Draw convincing pictures to show how the cycle number of g ◦ t differs from the cycle number of g. (b) Let t = [4 8]. Draw convincing pictures ...
HISTORICAL CONFLICTS AND SUBTLETIES WITH THE SIGN IN TEXTBOOKS
... The ambiguity of the square root is a problem with historical origins, as we can see in important and influential textbooks published at about the time the school system began to be reorganized into a general system of education, with repercussions as regards the way of organizing present-day elemen ...
... The ambiguity of the square root is a problem with historical origins, as we can see in important and influential textbooks published at about the time the school system began to be reorganized into a general system of education, with repercussions as regards the way of organizing present-day elemen ...
lesson 40 proportions
... Finally, “Fibonacci and phi are used in the design of violins and even in the design of high quality speaker wire!” Below is a snapshot of the Medici Violin that follows the golden ratio provided by our website with a few additions. It is up to the teacher’s discretion as to whether you want to spen ...
... Finally, “Fibonacci and phi are used in the design of violins and even in the design of high quality speaker wire!” Below is a snapshot of the Medici Violin that follows the golden ratio provided by our website with a few additions. It is up to the teacher’s discretion as to whether you want to spen ...
Mathematics and art

Mathematics and art are related in a variety of ways. Mathematics has itself been described as an art motivated by beauty. Mathematics can be discerned in arts such as music, dance, painting, architecture, sculpture, and textiles. This article focuses, however, on mathematics in the visual arts.Mathematics and art have a long historical relationship. Artists have used mathematics since the 5th century BC when the Greek sculptor Polykleitos wrote his Canon, prescribing proportions based on the ratio 1:√2 for the ideal male nude. Persistent popular claims have been made for the use of the golden ratio in ancient times, without reliable evidence. In the Italian Renaissance, Luca Pacioli wrote the influential treatise De Divina Proportione (1509), illustrated with woodcuts by Leonardo da Vinci, on the use of proportion in art. Another Italian painter, Piero della Francesca, developed Euclid's ideas on perspective in treatises such as De Prospectiva Pingendi, and in his paintings. The engraver Albrecht Dürer made many references to mathematics in his work Melencolia I. In modern times, the graphic artist M. C. Escher made intensive use of tessellation and hyperbolic geometry, with the help of the mathematician H. S. M. Coxeter, while the De Stijl movement led by Theo van Doesberg and Piet Mondrian explicitly embraced geometrical forms. Mathematics has inspired textile arts such as quilting, knitting, cross-stitch, crochet, embroidery, weaving, Turkish and other carpet-making, as well as kilim.Mathematics has directly influenced art with conceptual tools such as linear perspective, the analysis of symmetry and mathematical objects such as polyhedra and the Möbius strip. The construction of models of mathematical objects for research or teaching has led repeatedly to artwork, sometimes by mathematicians such as Magnus Wenninger who creates colourful stellated polyhedra. Mathematical concepts such as recursion and logical paradox can be seen in paintings by Rene Magritte, in engravings by M. C. Escher, and in computer art which often makes use of fractals, cellular automata and the Mandelbrot set. Controversially, the artist David Hockney has argued that artists from the Renaissance onwards made use of the camera lucida to draw precise representations of scenes; the architect Philip Steadman similarly argued that Vermeer used the camera obscura in his distinctively observed paintings.Other relationships include the algorithimic analysis of artworks by X-ray fluorescence spectroscopy; the stimulus to mathematics research by Filippo Brunelleschi's theory of perspective which eventually led to Girard Desargues's projective geometry; and the persistent view, based ultimately on the Pythagorean notion of harmony in music and the view that everything was arranged by Number, that God is the geometer of the world, and that the world's geometry is therefore sacred. This is seen in artworks such as William Blake's The Ancient of Days.