Basics of Open String Field Theory
... In a String Field Theory framework, the basic degrees of freedom are all the possible deformations (string fields) of a given reference conformal field theory one starts with. Such theories admit classical solutions which are in one–to–one correspondence to exact backgrounds of string theory which, ...
... In a String Field Theory framework, the basic degrees of freedom are all the possible deformations (string fields) of a given reference conformal field theory one starts with. Such theories admit classical solutions which are in one–to–one correspondence to exact backgrounds of string theory which, ...
Phase transition in gauge theories, monopoles and the Multiple
... Vef f (φc ) is a function of the classical field φc given by Vef f ...
... Vef f (φc ) is a function of the classical field φc given by Vef f ...
on the canonical formulation of electrodynamics and wave mechanics
... Nonperturbative methods for the solution of the coupled nonlinear MaxwellSchrödinger differential equations are developed in this dissertation which allow for the atomic or molecular and electromagnetic dynamics to occur on the same timescale. These equations have been derived within the Hamiltonia ...
... Nonperturbative methods for the solution of the coupled nonlinear MaxwellSchrödinger differential equations are developed in this dissertation which allow for the atomic or molecular and electromagnetic dynamics to occur on the same timescale. These equations have been derived within the Hamiltonia ...
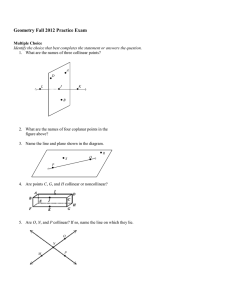
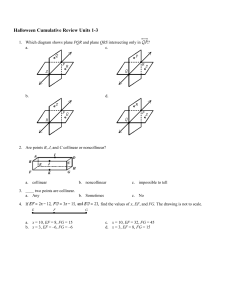
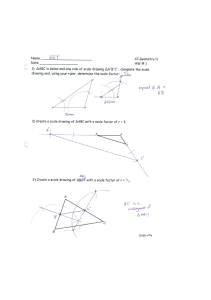
Review
... 5) Check answer to make sure it makes sense Test Taking Tips: Check your answer and make sure that it makes sense in the picture If the figure is smaller, then the corresponding part must be smaller than the given piece of the larger ...
... 5) Check answer to make sure it makes sense Test Taking Tips: Check your answer and make sure that it makes sense in the picture If the figure is smaller, then the corresponding part must be smaller than the given piece of the larger ...
Physics through Extra Dimensions: On Dualities, Unification, and Pair Production
... supersymmetric gauge theories with different gauge groups, with a fixed number of abelian factors. The quotients are such that the internal space has a finite, non-trivial fundamental group, and we construct a grand unified model in which the breaking of the gauge symmetry by Wilson lines to the sta ...
... supersymmetric gauge theories with different gauge groups, with a fixed number of abelian factors. The quotients are such that the internal space has a finite, non-trivial fundamental group, and we construct a grand unified model in which the breaking of the gauge symmetry by Wilson lines to the sta ...
Lattice QCD and String Theory Lattice 2005 Julius Kuti Confining Force
... and therefore should be built from physical objects, like the induced metric h ab = ∂ a X µ ∂ b X µ same determinant as Polyakov, but built from induced metric: ...
... and therefore should be built from physical objects, like the induced metric h ab = ∂ a X µ ∂ b X µ same determinant as Polyakov, but built from induced metric: ...
Reconstructing the dynamics of a movable mirror in a
... dynamics of a movable mirror in an optical cavity for arbitrary values of the detuning between the optical cavity and an input driving field. Our work, based on the use of linearized Langevin equations, allows for the exact reconstruction of the quantum statistical properties of the system at hand [ ...
... dynamics of a movable mirror in an optical cavity for arbitrary values of the detuning between the optical cavity and an input driving field. Our work, based on the use of linearized Langevin equations, allows for the exact reconstruction of the quantum statistical properties of the system at hand [ ...
Scale invariance

In physics, mathematics, statistics, and economics, scale invariance is a feature of objects or laws that do not change if scales of length, energy, or other variables, are multiplied by a common factor. The technical term for this transformation is a dilatation (also known as dilation), and the dilatations can also form part of a larger conformal symmetry.In mathematics, scale invariance usually refers to an invariance of individual functions or curves. A closely related concept is self-similarity, where a function or curve is invariant under a discrete subset of the dilatations. It is also possible for the probability distributions of random processes to display this kind of scale invariance or self-similarity.In classical field theory, scale invariance most commonly applies to the invariance of a whole theory under dilatations. Such theories typically describe classical physical processes with no characteristic length scale.In quantum field theory, scale invariance has an interpretation in terms of particle physics. In a scale-invariant theory, the strength of particle interactions does not depend on the energy of the particles involved.In statistical mechanics, scale invariance is a feature of phase transitions. The key observation is that near a phase transition or critical point, fluctuations occur at all length scales, and thus one should look for an explicitly scale-invariant theory to describe the phenomena. Such theories are scale-invariant statistical field theories, and are formally very similar to scale-invariant quantum field theories.Universality is the observation that widely different microscopic systems can display the same behaviour at a phase transition. Thus phase transitions in many different systems may be described by the same underlying scale-invariant theory.In general, dimensionless quantities are scale invariant. The analogous concept in statistics are standardized moments, which are scale invariant statistics of a variable, while the unstandardized moments are not.