2003 Exam
... Explain in detail what you know about the physics described by this equation with regards to a plane wave travelling in the dielectric medium (a derivation is not required, but please include in the explanation the meaning of each variable in the above formula). [7 marks] ...
... Explain in detail what you know about the physics described by this equation with regards to a plane wave travelling in the dielectric medium (a derivation is not required, but please include in the explanation the meaning of each variable in the above formula). [7 marks] ...
HW9
... 8. The diagram shows a horizontal 1.5m long copper rod weighing 40.0N suspended at its two ends by two wires attached to the ceiling. It is in a region where the magnetic field is 2.4T pointing into the paper. A current runs in the rod. What must be the direction and magnitude of the current so that ...
... 8. The diagram shows a horizontal 1.5m long copper rod weighing 40.0N suspended at its two ends by two wires attached to the ceiling. It is in a region where the magnetic field is 2.4T pointing into the paper. A current runs in the rod. What must be the direction and magnitude of the current so that ...
Atomic Units
... 1, where me is the mass of the electron. Then c = 1/α = 137 is a big number in atomic units. This is appropriate, since the electron’s “natural” speed, in the ground state of hydrogen, is 137 times slower than c. Table I summarizes conversion factors between atomic units, cgs “Gaussian” units, and M ...
... 1, where me is the mass of the electron. Then c = 1/α = 137 is a big number in atomic units. This is appropriate, since the electron’s “natural” speed, in the ground state of hydrogen, is 137 times slower than c. Table I summarizes conversion factors between atomic units, cgs “Gaussian” units, and M ...
3 Maxwell`s equations and material equations
... the third equations are independently known as Gauss’ law for electrostatics and magnetostatics respectively. When we write them in Maxwell’s equation the status of these are raised from statics to dynamics. In other words the laws are valid even if the charges are moving. The second equation is not ...
... the third equations are independently known as Gauss’ law for electrostatics and magnetostatics respectively. When we write them in Maxwell’s equation the status of these are raised from statics to dynamics. In other words the laws are valid even if the charges are moving. The second equation is not ...
This is a test given in the past - it... - it is not meant for practice and these particular...
... 5. Each of three objects has a net charge. Objects A and B attract one another. Objects B and C also attract one another, but objects A and C repel one another. Which one of the following table entries is a possible combination of the signs of the net charges on these three objects? (4) ...
... 5. Each of three objects has a net charge. Objects A and B attract one another. Objects B and C also attract one another, but objects A and C repel one another. Which one of the following table entries is a possible combination of the signs of the net charges on these three objects? (4) ...
Document
... a. will continue moving at the same velocity unless an outside force acts on it b. will continue moving in a straight line unless an outside force acts on it c. at rest will remain at rest unless acted on by an outside force d. all of the above If the force of gravity suddenly stopped acting on the ...
... a. will continue moving at the same velocity unless an outside force acts on it b. will continue moving in a straight line unless an outside force acts on it c. at rest will remain at rest unless acted on by an outside force d. all of the above If the force of gravity suddenly stopped acting on the ...
Exam 1 Coverage
... (a) Similar to Problem 1 in the WebAssign HW Set 1: two electric charges suspended by light strings and in equilibrium. (b) Similar to Problem 2 in the WebAssign HW Set 1: With two charges fixed in position, find a point on the line through them where a third charge would be in equilibrium (or, in o ...
... (a) Similar to Problem 1 in the WebAssign HW Set 1: two electric charges suspended by light strings and in equilibrium. (b) Similar to Problem 2 in the WebAssign HW Set 1: With two charges fixed in position, find a point on the line through them where a third charge would be in equilibrium (or, in o ...
HERE. - Lnk2Lrn
... The name probably comes from Magnesia, but there is a fable of Magnes, a Greek shepherd, who discovered magnetite when the nails in his shoes stuck to the ground! ...
... The name probably comes from Magnesia, but there is a fable of Magnes, a Greek shepherd, who discovered magnetite when the nails in his shoes stuck to the ground! ...
Homework 1 Solution
... A note about the solution to the graded problem. A solution should contain a short explanation about what you are doing at every physics step. You don’t have to explain the math steps. Also, show the physics equations you are using before you use them. Lay out the value for each variable before the ...
... A note about the solution to the graded problem. A solution should contain a short explanation about what you are doing at every physics step. You don’t have to explain the math steps. Also, show the physics equations you are using before you use them. Lay out the value for each variable before the ...
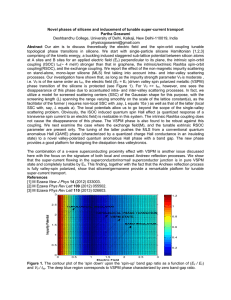
2016_Goswami_Partha_physicsgoswami@gmail
... not cause the disappearance of this phase. The VSPM phase is also found to be robust against this coupling. We next examine the case where the exchange field(M), and the tunable extrinsic RSOC parameter are present only. The tuning of the latter pushes the MLS from a conventional quantum anomalous H ...
... not cause the disappearance of this phase. The VSPM phase is also found to be robust against this coupling. We next examine the case where the exchange field(M), and the tunable extrinsic RSOC parameter are present only. The tuning of the latter pushes the MLS from a conventional quantum anomalous H ...
Field (physics)
In physics, a field is a physical quantity that has a value for each point in space and time. For example, on a weather map, the surface wind velocity is described by assigning a vector to each point on a map. Each vector represents the speed and direction of the movement of air at that point. As another example, an electric field can be thought of as a ""condition in space"" emanating from an electric charge and extending throughout the whole of space. When a test electric charge is placed in this electric field, the particle accelerates due to a force. Physicists have found the notion of a field to be of such practical utility for the analysis of forces that they have come to think of a force as due to a field.In the modern framework of the quantum theory of fields, even without referring to a test particle, a field occupies space, contains energy, and its presence eliminates a true vacuum. This lead physicists to consider electromagnetic fields to be a physical entity, making the field concept a supporting paradigm of the edifice of modern physics. ""The fact that the electromagnetic field can possess momentum and energy makes it very real... a particle makes a field, and a field acts on another particle, and the field has such familiar properties as energy content and momentum, just as particles can have"". In practice, the strength of most fields has been found to diminish with distance to the point of being undetectable. For instance the strength of many relevant classical fields, such as the gravitational field in Newton's theory of gravity or the electrostatic field in classical electromagnetism, is inversely proportional to the square of the distance from the source (i.e. they follow the Gauss's law). One consequence is that the Earth's gravitational field quickly becomes undetectable on cosmic scales.A field can be classified as a scalar field, a vector field, a spinor field or a tensor field according to whether the represented physical quantity is a scalar, a vector, a spinor or a tensor, respectively. A field has a unique tensorial character in every point where it is defined: i.e. a field cannot be a scalar field somewhere and a vector field somewhere else. For example, the Newtonian gravitational field is a vector field: specifying its value at a point in spacetime requires three numbers, the components of the gravitational field vector at that point. Moreover, within each category (scalar, vector, tensor), a field can be either a classical field or a quantum field, depending on whether it is characterized by numbers or quantum operators respectively. In fact in this theory an equivalent representation of field is a field particle, namely a boson.