mathematical logic: constructive and non
... Early in the century, especially in connection with Hubert's treatment of geometry (1899), it was being said t h a t the theorems of an axiomatic theory express truths about whatever systems of objects make the axioms true. I n the simplest case, a system S consists of a non-empty set D (the domain) ...
... Early in the century, especially in connection with Hubert's treatment of geometry (1899), it was being said t h a t the theorems of an axiomatic theory express truths about whatever systems of objects make the axioms true. I n the simplest case, a system S consists of a non-empty set D (the domain) ...
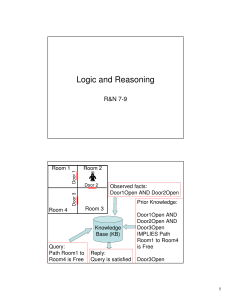
Logic and Reasoning
... • An inference algorithm is a procedure for deriving a sentence from the KB • KB |-i S means that S is inferred from KB using algorithm i. • The inference algorithm is sound if it derives only sentences that are entailed by KB. • The inference algorithm is complete if it can derive any sentence that ...
... • An inference algorithm is a procedure for deriving a sentence from the KB • KB |-i S means that S is inferred from KB using algorithm i. • The inference algorithm is sound if it derives only sentences that are entailed by KB. • The inference algorithm is complete if it can derive any sentence that ...
Document
... Arguments in Proposi:onal Logic • A argument in proposi:onal logic is a sequence of proposi:ons. All but the final proposi:on are called premises. The last statement is the conclusion. • The argument is valid if the premises imply the conclusion. An argument form is an argument that is ...
... Arguments in Proposi:onal Logic • A argument in proposi:onal logic is a sequence of proposi:ons. All but the final proposi:on are called premises. The last statement is the conclusion. • The argument is valid if the premises imply the conclusion. An argument form is an argument that is ...
THE PARADOXES OF STRICT IMPLICATION John L
... s e s to do with one another, if, that is, A and B are totally disparate in meaning," It cannot be denied that there is a strong temptation to identify implication with a relation between meanings. However, we must be more explicit about just what this relation is. Let us begin with the case of anal ...
... s e s to do with one another, if, that is, A and B are totally disparate in meaning," It cannot be denied that there is a strong temptation to identify implication with a relation between meanings. However, we must be more explicit about just what this relation is. Let us begin with the case of anal ...
REASONING WITH ASSERTIONS AND EXAMPLES a
... true if the representation of the typical bird Tweety contains the information that Tweety can, in fact, fly. In other words, we have two different levels of information: the syntactic information, bird(Birdy), which stated in the object language, where (deductive) inferences are drawn, and the sema ...
... true if the representation of the typical bird Tweety contains the information that Tweety can, in fact, fly. In other words, we have two different levels of information: the syntactic information, bird(Birdy), which stated in the object language, where (deductive) inferences are drawn, and the sema ...
MAT 300 Mathematical Structures
... out the proof, and then we will write up the formal proof. None of the scratch work can be used in the proof itself. One consequence of this is that in our scratch work we are allowed to state things informally, and even sometimes not quite completely correctly! The proof must stand completely on it ...
... out the proof, and then we will write up the formal proof. None of the scratch work can be used in the proof itself. One consequence of this is that in our scratch work we are allowed to state things informally, and even sometimes not quite completely correctly! The proof must stand completely on it ...
x - WordPress.com
... humans. Human beings make decisions based on rules. Although, we may not be aware of it, all the decisions we make are all based on computer like if-then statements. If the weather is fine, then we may decide to go out. If the forecast stays the weather will be bad today, but fine tomorrow, then we ...
... humans. Human beings make decisions based on rules. Although, we may not be aware of it, all the decisions we make are all based on computer like if-then statements. If the weather is fine, then we may decide to go out. If the forecast stays the weather will be bad today, but fine tomorrow, then we ...
Notes on `the contemporary conception of logic`
... of the schema. But the sentence ‘Either grass is green or grass is not green’ – at least once we pre-process it as ‘Grass is green ∨ ¬ grass is green’ – is an instance of both the schema P ∨ ¬P and the schema Q ∨ ¬Q. These are two different schemata (if we indeed think of schemata, as Goldfarb descr ...
... of the schema. But the sentence ‘Either grass is green or grass is not green’ – at least once we pre-process it as ‘Grass is green ∨ ¬ grass is green’ – is an instance of both the schema P ∨ ¬P and the schema Q ∨ ¬Q. These are two different schemata (if we indeed think of schemata, as Goldfarb descr ...
PDF
... Call a wff of FO(Σ) quasi-atom if it is either atomic, or of the form ∀xA, where A is a wff of FO(Σ). Let Γ be the set of all quasi-atoms of FO(Σ). Proposition 1. Every wff of FO(Σ) can be uniquely built up from Γ using only logical connectives → and ¬. Proof. Induction on the complexity of wff. For ...
... Call a wff of FO(Σ) quasi-atom if it is either atomic, or of the form ∀xA, where A is a wff of FO(Σ). Let Γ be the set of all quasi-atoms of FO(Σ). Proposition 1. Every wff of FO(Σ) can be uniquely built up from Γ using only logical connectives → and ¬. Proof. Induction on the complexity of wff. For ...
Document
... Conjunction is a binary operator in that it operates on two propositions when creating compound proposition. On the other hand, negation is a unary operator (the only non-trivial one possible). ...
... Conjunction is a binary operator in that it operates on two propositions when creating compound proposition. On the other hand, negation is a unary operator (the only non-trivial one possible). ...
Normalised and Cut-free Logic of Proofs
... be obtained in the logic of proofs with an intuitionistic base. Indeed, for Ilp too, we can prove the deduction theorem, the substitution lemma and the internalisation of proofs. Moreover, Ilp is sound and complete with respect to the modal logic S4 with an intuitionistic base, and with respect to H ...
... be obtained in the logic of proofs with an intuitionistic base. Indeed, for Ilp too, we can prove the deduction theorem, the substitution lemma and the internalisation of proofs. Moreover, Ilp is sound and complete with respect to the modal logic S4 with an intuitionistic base, and with respect to H ...
How to tell the truth without knowing what you are talking about
... negation in Standard English (“I do not want nothing” means that I want something), but different from some other natural languages, such as Italian or French, where it is customary that a double negation negates (“Non voglio niente” and “Je ne veux rien” both mean that I do not want anything), or s ...
... negation in Standard English (“I do not want nothing” means that I want something), but different from some other natural languages, such as Italian or French, where it is customary that a double negation negates (“Non voglio niente” and “Je ne veux rien” both mean that I do not want anything), or s ...
Lecture 1: Elements of Mathematical Logic
... rigorous and meticulous; but we will take our time to cover the material. And while we will be often dealing in abstractions; we shall be doing so to develop concrete ways of handling far reaching concepts. 1. Basic Logic 1.1. Statements. In order to get our bearings, let us begin with a discussion ...
... rigorous and meticulous; but we will take our time to cover the material. And while we will be often dealing in abstractions; we shall be doing so to develop concrete ways of handling far reaching concepts. 1. Basic Logic 1.1. Statements. In order to get our bearings, let us begin with a discussion ...
Lecture - 04 (Logic Knowledge Base)
... called premises and another proposition called the conclusion. • Proof is intended to show deductively that an argument is sound (or valid). – An argument is sound iff it cannot be the case that its premises are true and its conclusion is false. ...
... called premises and another proposition called the conclusion. • Proof is intended to show deductively that an argument is sound (or valid). – An argument is sound iff it cannot be the case that its premises are true and its conclusion is false. ...
Propositional Logic
... contained. Also, logical reasoning methods are designed to work no matter what meanings or values are assigned to the logical “variables” used in sentences. Although the values assigned to variables are not crucial in the sense just described, in talking about logic itself, it is sometimes useful t ...
... contained. Also, logical reasoning methods are designed to work no matter what meanings or values are assigned to the logical “variables” used in sentences. Although the values assigned to variables are not crucial in the sense just described, in talking about logic itself, it is sometimes useful t ...
Q - GROU.PS
... conducting proofs and program verification, but also for artificial intelligence systems (drawing logical inferences from knowledge and facts). We focus on deductive proofs Spring 2003 ...
... conducting proofs and program verification, but also for artificial intelligence systems (drawing logical inferences from knowledge and facts). We focus on deductive proofs Spring 2003 ...
Divide and congruence applied to eta-bisimulation
... processes that take into account the internal action τ . Here we focus on one such equivalence, called η-bisimulation [1]. In general a semantic equivalence induced by a transition system specification is not a congruence, i.e. the equivalence class of a term f (p1 , . . . , pn ) need not be determi ...
... processes that take into account the internal action τ . Here we focus on one such equivalence, called η-bisimulation [1]. In general a semantic equivalence induced by a transition system specification is not a congruence, i.e. the equivalence class of a term f (p1 , . . . , pn ) need not be determi ...
INTRODUCTION TO LOGIC Natural Deduction
... The existence of such a set of rules is remarkable for various reasons: In order to prove that an argument in L is valid, one can use the proof system. An alternative definition of the validity of arguments becomes available: An argument is valid iff the conclusion can be derived from the premisses ...
... The existence of such a set of rules is remarkable for various reasons: In order to prove that an argument in L is valid, one can use the proof system. An alternative definition of the validity of arguments becomes available: An argument is valid iff the conclusion can be derived from the premisses ...
relevant reasoning as the logical basis of
... extensional notion of material implication (denoted by → in this paper) which is defined as A→B =df ¬(A∧¬B) or A→B =df ¬A∨B. However, the material implication is just a truth-function of its antecedent and consequent but not requires that there must exist a necessarily relevant and/or conditional re ...
... extensional notion of material implication (denoted by → in this paper) which is defined as A→B =df ¬(A∧¬B) or A→B =df ¬A∨B. However, the material implication is just a truth-function of its antecedent and consequent but not requires that there must exist a necessarily relevant and/or conditional re ...
Lecture 6 Induction
... Let’s try it for some small values of n. n = 1 (1 = 12), n = 2 (1+ 3 = 4 = 22), n = 3 (1 + 3 + 5 = 9 = 32) This is NOT A PROOF! These simply show that the propositions P(1), P(2) and P(3) are true. This fact will be useful for proving that the sum of the first n odd numbers is n2. ...
... Let’s try it for some small values of n. n = 1 (1 = 12), n = 2 (1+ 3 = 4 = 22), n = 3 (1 + 3 + 5 = 9 = 32) This is NOT A PROOF! These simply show that the propositions P(1), P(2) and P(3) are true. This fact will be useful for proving that the sum of the first n odd numbers is n2. ...
Chapter 1: The Foundations: Logic and Proofs
... Tautology: A compound proposition that is always true. Contradiction: A compound proposition that is always false. Contingency: A compound proposition that is neither a tautology nor a contradiction. ...
... Tautology: A compound proposition that is always true. Contradiction: A compound proposition that is always false. Contingency: A compound proposition that is neither a tautology nor a contradiction. ...
Knowledge representation 1
... variable and in the other case a constant, substitute the constant for the variable, everywhere that that constant appears in the clause. ...
... variable and in the other case a constant, substitute the constant for the variable, everywhere that that constant appears in the clause. ...
slides
... Idea of a (propositional) logic program A logic program is given by a list of (propositional) formulas F1 , F2 , . . . , Fn . A goal is given by another formula G . The task of the system is to determine whether F1 , . . . , Fn |= G . If so, the system returns ‘yes’. Otherwise the system returns ‘n ...
... Idea of a (propositional) logic program A logic program is given by a list of (propositional) formulas F1 , F2 , . . . , Fn . A goal is given by another formula G . The task of the system is to determine whether F1 , . . . , Fn |= G . If so, the system returns ‘yes’. Otherwise the system returns ‘n ...
Oh Yeah? Well, Prove It.
... A large part of mathematics consists of building up a theoretical framework that allows us to solve problems. This theoretical framework is built upon a set of axioms. Axioms are unproven assumptions that are the foundation of all mathematics. (Not everyone agrees on what axioms should be used, but ...
... A large part of mathematics consists of building up a theoretical framework that allows us to solve problems. This theoretical framework is built upon a set of axioms. Axioms are unproven assumptions that are the foundation of all mathematics. (Not everyone agrees on what axioms should be used, but ...