1. With linear functions as x increases by
... dropped ball in feet after its xth bounce. On which bounce was the height of the ...
... dropped ball in feet after its xth bounce. On which bounce was the height of the ...
7.6 Modeling Data: Exponential, Logarithmic, and Quadratic Functions
... a logarithmic model y = a + b (ln x), where ln x is called the natural logarithm. a. Express the model in function notation, with numbers rounded to one decimal place. • f(x) = -11.6 + 13.4 ln x b. Use the function to find temperature increase, to the ...
... a logarithmic model y = a + b (ln x), where ln x is called the natural logarithm. a. Express the model in function notation, with numbers rounded to one decimal place. • f(x) = -11.6 + 13.4 ln x b. Use the function to find temperature increase, to the ...
Document
... 1. A number in (standard form, scientific notation) is written as a product of two factors in the form a 3 10n, where n is an integer and 1 # a , 10. 2. Each number in a sequence is called a (term, constant). 3. In a(n) (arithmetic, geometric) sequence you multiply a term in the sequence by a fixed ...
... 1. A number in (standard form, scientific notation) is written as a product of two factors in the form a 3 10n, where n is an integer and 1 # a , 10. 2. Each number in a sequence is called a (term, constant). 3. In a(n) (arithmetic, geometric) sequence you multiply a term in the sequence by a fixed ...
STAT 315: LECTURE 4 CHAPTER 4: CONTINUOUS RANDOM
... Probably the most systematic eyeball method is to look at a normal probability plot (a.k.a. QQ plot). This is actually a decent method for determining which named distribution (normal, uniform, exponential, or other) should be parametrically fit (by using data to estimate the parameters defining the ...
... Probably the most systematic eyeball method is to look at a normal probability plot (a.k.a. QQ plot). This is actually a decent method for determining which named distribution (normal, uniform, exponential, or other) should be parametrically fit (by using data to estimate the parameters defining the ...
File
... To multiply numbers with the same base, keep the base and add the exponents. To divide numbers with the same base, keep the base and subtract the exponents. When raising a power to a power, keep the base and multiply the exponents. The power of a product is the product of the powers. ...
... To multiply numbers with the same base, keep the base and add the exponents. To divide numbers with the same base, keep the base and subtract the exponents. When raising a power to a power, keep the base and multiply the exponents. The power of a product is the product of the powers. ...
Do Now Lesson #10 – Rules of Exponents Part 2 **Rule - Math
... Any number with a zero as the exponent is equal to 1. Power of One Any number with a 1 as the exponent is equal to itself. Negative Exponents If an exponent is negative, you take the reciprocal of the exponential number and make the exponent positive. Now, You Try! 4) Write (73 )6 in simplest expone ...
... Any number with a zero as the exponent is equal to 1. Power of One Any number with a 1 as the exponent is equal to itself. Negative Exponents If an exponent is negative, you take the reciprocal of the exponential number and make the exponent positive. Now, You Try! 4) Write (73 )6 in simplest expone ...
Exponential Functions
... In this lecture, we introduce the exponential functions, which is the third major type of function we will study in this class. Before we can study the exponential functions, we need to review the rules of exponentiation and taking logarithms. Let a and b be two real numbers with a > 0. If b is a na ...
... In this lecture, we introduce the exponential functions, which is the third major type of function we will study in this class. Before we can study the exponential functions, we need to review the rules of exponentiation and taking logarithms. Let a and b be two real numbers with a > 0. If b is a na ...
Exponential Form of a Complex Number Lab
... efore we can investigate the exponential form of a complex number, we'll have to do some preliminary work. Much of it is based on work done by the remarkable mathematician Leonard Euler. We are first going to define the number e (through the use of the binomial theorem). Then, with the help of Euler ...
... efore we can investigate the exponential form of a complex number, we'll have to do some preliminary work. Much of it is based on work done by the remarkable mathematician Leonard Euler. We are first going to define the number e (through the use of the binomial theorem). Then, with the help of Euler ...
Week 2
... • The domain of y = ax consists of all real numbers, and the range consists of all positive numbers. All exponential functions have graphs that pass through the point (0, 1), are concave up, and lie entirely above the x-axis. • If 0 < a < 1, then the output of f decreases as the input increases and ...
... • The domain of y = ax consists of all real numbers, and the range consists of all positive numbers. All exponential functions have graphs that pass through the point (0, 1), are concave up, and lie entirely above the x-axis. • If 0 < a < 1, then the output of f decreases as the input increases and ...
lesson - Garnet Valley School District
... Name ___________________________________________ Date _____________________ Class ____________________ ...
... Name ___________________________________________ Date _____________________ Class ____________________ ...
4.3: Introduction to Logarithmic Functions
... Name ___________________________________________ Date _____________________ Class ____________________ ...
... Name ___________________________________________ Date _____________________ Class ____________________ ...
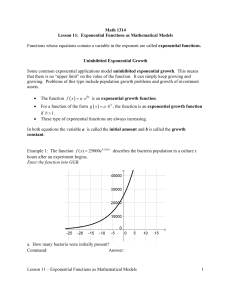
Lesson 11 – Exponential Functions as Mathematical Models 1 Math
... Limited Growth Models A worker on an assembly line performs the same task repeatedly throughout the workday. With experience, the worker will perform at or near an optimal level. However, when first learning to do the task, the worker’s productivity will be much lower. During these early experience ...
... Limited Growth Models A worker on an assembly line performs the same task repeatedly throughout the workday. With experience, the worker will perform at or near an optimal level. However, when first learning to do the task, the worker’s productivity will be much lower. During these early experience ...
The exponential function
... The most important and widely used exponential function has the particular base 2.7182818 . . . , a number always denoted by the single letter e: e = 2.7182818 . . . It will not be clear to the reader why this particular value is so important. However, its importance will become clear as your knowl ...
... The most important and widely used exponential function has the particular base 2.7182818 . . . , a number always denoted by the single letter e: e = 2.7182818 . . . It will not be clear to the reader why this particular value is so important. However, its importance will become clear as your knowl ...
exponential functions
... setting two equations equal to each other and finding the value of x that satisfies both equations. We could then substitute the solution (the x) into either equation and find the “y” of that point. • Make up two equation, set them equal to each other, and show what “equal” means geometrically on ge ...
... setting two equations equal to each other and finding the value of x that satisfies both equations. We could then substitute the solution (the x) into either equation and find the “y” of that point. • Make up two equation, set them equal to each other, and show what “equal” means geometrically on ge ...
Understanding By Design Unit Template
... b. Use the properties of exponents to interpret expressions for exponential functions. For example, identify percent rate of change in functions such as y = (1.02)t, y = (0.97)t, y = (1.01)12t, y = (1.2)t/10, and classify them as representing exponential growth or decay. F.BF.1Write a function that ...
... b. Use the properties of exponents to interpret expressions for exponential functions. For example, identify percent rate of change in functions such as y = (1.02)t, y = (0.97)t, y = (1.01)12t, y = (1.2)t/10, and classify them as representing exponential growth or decay. F.BF.1Write a function that ...
exponential function
... In the exponential function found by Excel to model the toad data, the coefficient of the exponential term was given as 9E-62. This number is to be interpreted as 9*10^(-62), which is in scientific notation. Recall that multiplying a number by an integer power of 10 moves the decimal place right ...
... In the exponential function found by Excel to model the toad data, the coefficient of the exponential term was given as 9E-62. This number is to be interpreted as 9*10^(-62), which is in scientific notation. Recall that multiplying a number by an integer power of 10 moves the decimal place right ...
Inverse of An Exponential Function Since an exponential function, f
... Inverse of An Exponential Function Since an exponential function, f(x) = bx, is an 1-1 function, it has an inverse. ...
... Inverse of An Exponential Function Since an exponential function, f(x) = bx, is an 1-1 function, it has an inverse. ...
hw2.pdf
... My understanding is that two breeding populations were raised generation after generation on the same diet C or S, but the flies destined for experimental purposes were removed from the breeding population and raised for one intermediate generation on the CMY diet before testing. Thus the testing fo ...
... My understanding is that two breeding populations were raised generation after generation on the same diet C or S, but the flies destined for experimental purposes were removed from the breeding population and raised for one intermediate generation on the CMY diet before testing. Thus the testing fo ...
Lecture notes for Section 9.2 (Exponential Functions)
... Big Idea: The exponential function is a base raised to a power that is a variable. Big Skill: You should be able to graph an exponential function, solve basic exponential equations, and use exponential function models. Definition: Exponential Function An exponential function is a function of the for ...
... Big Idea: The exponential function is a base raised to a power that is a variable. Big Skill: You should be able to graph an exponential function, solve basic exponential equations, and use exponential function models. Definition: Exponential Function An exponential function is a function of the for ...
INSTITUTE OF ACTUARIES OF INDIA EXAMINATIONS 22
... (ii) A no claims discount (NCD) system has three states 0%, 20% and 50%. The full premium for a policyholder in the system is Rs 800. Any policyholder making a claim in any year moves to the next lower discount level (or stays on 0%). Any policyholder who does not make a claim during a year moves in ...
... (ii) A no claims discount (NCD) system has three states 0%, 20% and 50%. The full premium for a policyholder in the system is Rs 800. Any policyholder making a claim in any year moves to the next lower discount level (or stays on 0%). Any policyholder who does not make a claim during a year moves in ...
An Exponential Function with base b is a function of the form: f(x
... We know the meaning of br if r is a rational number. What if r is irrational? What we do is we approximate the value of br by using rational approximate for r. For example, to approximate 5π , we may approximate it as 53.12 , 53.141 , 53.1415 , 53.14159 .... In advance mathematics one can define the ...
... We know the meaning of br if r is a rational number. What if r is irrational? What we do is we approximate the value of br by using rational approximate for r. For example, to approximate 5π , we may approximate it as 53.12 , 53.141 , 53.1415 , 53.14159 .... In advance mathematics one can define the ...
b x = . log log x x = ln x = 9 3 = 1 5 125 = 2401 7 = log 8
... 3. You try it: f t 10 0.987 to the form Q t Q0e kt ...
... 3. You try it: f t 10 0.987 to the form Q t Q0e kt ...
What is the domain of an exponential function?
... need a base that turns out to be between 2 and 3. Your calculator knows this base. Ask your calculator to find e1. You do this by using the ex button (generally you’ll need to hit the 2nd or yellow button first to get it depending on the calculator). After hitting the ex, you then enter the exponent ...
... need a base that turns out to be between 2 and 3. Your calculator knows this base. Ask your calculator to find e1. You do this by using the ex button (generally you’ll need to hit the 2nd or yellow button first to get it depending on the calculator). After hitting the ex, you then enter the exponent ...
5.4 Dividing Monomials: The Quotient Rule and Integer Exponents
... 5.4 Dividing Polynomials: The Quotient Rule and Integer Exponents Learning Objectives: 1. Exponential Properties. 2. Simplify using Exponential Properties. 3. Simplify exponential expressions using the Laws of Exponents. ...
... 5.4 Dividing Polynomials: The Quotient Rule and Integer Exponents Learning Objectives: 1. Exponential Properties. 2. Simplify using Exponential Properties. 3. Simplify exponential expressions using the Laws of Exponents. ...
Logarithms and Exponential Functions PowerPoint
... appears as though the graph stops at x = 2; it does not!! The graph continues down forever; the range is all real numbers. Keep this in mind at all times!! ...
... appears as though the graph stops at x = 2; it does not!! The graph continues down forever; the range is all real numbers. Keep this in mind at all times!! ...