3-1
... mall after x hours. What is the average amount spent, to the nearest dollar, after three hours at a shopping mall? We substitute 3 for x and evaluate the function. f ( x) 42.2(1.56) x f (3) 42.2(1.56)3 160.20876 160 After 3 hours at a shopping mall, the average amount spent is $160. Copyrigh ...
... mall after x hours. What is the average amount spent, to the nearest dollar, after three hours at a shopping mall? We substitute 3 for x and evaluate the function. f ( x) 42.2(1.56) x f (3) 42.2(1.56)3 160.20876 160 After 3 hours at a shopping mall, the average amount spent is $160. Copyrigh ...
Exponential Notation - Gordon State College
... how to convert a number to exponential notation, consider the following example. Example: Write 125000 in exponential notatioa The standard format for exponential notation uses a factor between 1 and 10 that gives all the appropriate significant digits of the number, multiplied by a power of ten tha ...
... how to convert a number to exponential notation, consider the following example. Example: Write 125000 in exponential notatioa The standard format for exponential notation uses a factor between 1 and 10 that gives all the appropriate significant digits of the number, multiplied by a power of ten tha ...
CH6 Section 6.1
... The output values for the exponential function grow much faster. Increasing the x-values by one in the linear function has the effect of adding 3 more units to the value of f(x), whereas increasing the x-values by one in the exponential function has the effect of multiplying g(x) by the growth facto ...
... The output values for the exponential function grow much faster. Increasing the x-values by one in the linear function has the effect of adding 3 more units to the value of f(x), whereas increasing the x-values by one in the exponential function has the effect of multiplying g(x) by the growth facto ...
Chapter 9: Exponential and Log. Functions Lecture notes Math 1010
... (1) In the equation for f (x), replace f (x) with y. (2) Interchange x and y. (3) If the new equation does not represent y as a function of x, the function f does not have an inverse function. If the new equation does represent y as a function of x, solve the new equation for y. (4) Replace y with f ...
... (1) In the equation for f (x), replace f (x) with y. (2) Interchange x and y. (3) If the new equation does not represent y as a function of x, the function f does not have an inverse function. If the new equation does represent y as a function of x, solve the new equation for y. (4) Replace y with f ...
Exponential Notation
... An exponent of 2 or greater tells how many times the base is used as a factor. For example, a a a a = a4 : In this case, the exponent is 4 and the base is a. An expression for a power is called exponential notation. ...
... An exponent of 2 or greater tells how many times the base is used as a factor. For example, a a a a = a4 : In this case, the exponent is 4 and the base is a. An expression for a power is called exponential notation. ...
3 Exponential and Logarithmic functions
... we have not defined 2x when x is irrational, the√ graph above actually has a hole in it above every irrational number, such as 3. We remedy this situation by defining 2x for irrational x in such a way that the graph is smooth. (This informal way of extending f to the irrational numbers will be suita ...
... we have not defined 2x when x is irrational, the√ graph above actually has a hole in it above every irrational number, such as 3. We remedy this situation by defining 2x for irrational x in such a way that the graph is smooth. (This informal way of extending f to the irrational numbers will be suita ...
Document
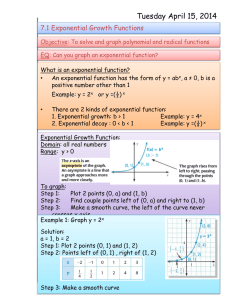
... To see the basic shape of the graph of an exponential decay function, you can make a table of values and plot points, as shown below. x Notice the end behavior of graph. 1 the x f(x) = (2) As x –, f(x) +, which means ...
... To see the basic shape of the graph of an exponential decay function, you can make a table of values and plot points, as shown below. x Notice the end behavior of graph. 1 the x f(x) = (2) As x –, f(x) +, which means ...
A numerical characteristic of extreme values
... Rapidly varying tail distributions are various. · Very rapid tail decay : the normal distribution and the Rayleigh distribution. · Middle tail decay: the exponential type, i.e. the exponential distribution, the Gamma distribution, the Chi-square distribution, the generalized inverse Gaussian distri ...
... Rapidly varying tail distributions are various. · Very rapid tail decay : the normal distribution and the Rayleigh distribution. · Middle tail decay: the exponential type, i.e. the exponential distribution, the Gamma distribution, the Chi-square distribution, the generalized inverse Gaussian distri ...
Document
... • He offered them the choice of $1,000,000.00 cash or • $.01 cash (yes, ONE Penny) that would double everyday for one month (30 days). He then sent them home to consider the offer. • Which choice is better? Why? ...
... • He offered them the choice of $1,000,000.00 cash or • $.01 cash (yes, ONE Penny) that would double everyday for one month (30 days). He then sent them home to consider the offer. • Which choice is better? Why? ...
Algorithms for Distributions
... (with replacement) one element from a setPof K elements. For example a random variable X having the n B(n, p) distribution can be written as X = i=1 Yi where each of the Y ’s is either one (with probability p) or zero (with probability 1 − p). A multinomial random vector (X1 , . . . , Xk ) with n tr ...
... (with replacement) one element from a setPof K elements. For example a random variable X having the n B(n, p) distribution can be written as X = i=1 Yi where each of the Y ’s is either one (with probability p) or zero (with probability 1 − p). A multinomial random vector (X1 , . . . , Xk ) with n tr ...
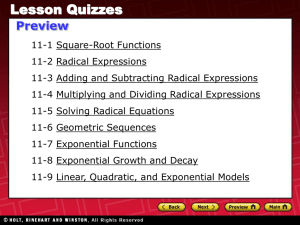
ch11_quiz
... 1. The number of employees at a certain company is 1440 and is increasing at a rate of 1.5% per year. Write an exponential growth function to model this situation. Then find the number of employees in the company after 9 years. y = 1440(1.015)t; 1646 Write a compound interest function to model each ...
... 1. The number of employees at a certain company is 1440 and is increasing at a rate of 1.5% per year. Write an exponential growth function to model this situation. Then find the number of employees in the company after 9 years. y = 1440(1.015)t; 1646 Write a compound interest function to model each ...
Exponential Functions
... wise person asks the king for a single grain of rice to be placed on the first square of a chessboard, two grains on the next square, four grains in the square after that, and so on, with the number of grains of rice doubling with each sequential square. In every version, the king is surprised by su ...
... wise person asks the king for a single grain of rice to be placed on the first square of a chessboard, two grains on the next square, four grains in the square after that, and so on, with the number of grains of rice doubling with each sequential square. In every version, the king is surprised by su ...
MA123, Supplement: Exponential and logarithmic functions (pp. 315
... The number a is called the base whereas n is called the exponent. The first and second laws of exponents below allow us to define an for any integer n. Now, we want to define, for instance, a1/3 in a way that Definition of rational exponents: For any is consistent with the laws of exponents. We woul ...
... The number a is called the base whereas n is called the exponent. The first and second laws of exponents below allow us to define an for any integer n. Now, we want to define, for instance, a1/3 in a way that Definition of rational exponents: For any is consistent with the laws of exponents. We woul ...
MA123, Supplement: Exponential and logarithmic functions (pp. 315
... In other words, loga (x) is the exponent to which the base a must be raised to give x. ...
... In other words, loga (x) is the exponent to which the base a must be raised to give x. ...
Basic Exponents - K and B Tutoring
... In the table below, the number 2 is written as a factor repeatedly. The product of factors is also displayed in this table. Suppose that your teacher asked you to Write 2 as a factor one million times for homework. How long do you think that would take? Answer ...
... In the table below, the number 2 is written as a factor repeatedly. The product of factors is also displayed in this table. Suppose that your teacher asked you to Write 2 as a factor one million times for homework. How long do you think that would take? Answer ...
1 Definitions of powers and exponential expressions
... Other examples in which exponents are used to show powers are given below. - 42 is four to the second power (or 4 squared) and means 4 × 4, or 16. - 103 is ten to the third power (or 10 cubed) and means 10 × 10 × 10, or 1000. - a6 is a to the sixth power and means a × a × a × a × a × a. A number rai ...
... Other examples in which exponents are used to show powers are given below. - 42 is four to the second power (or 4 squared) and means 4 × 4, or 16. - 103 is ten to the third power (or 10 cubed) and means 10 × 10 × 10, or 1000. - a6 is a to the sixth power and means a × a × a × a × a × a. A number rai ...
CONVERGENCE IN DISTRIBUTION !F)!F)!F)!F)!F)!F)!F)!F)!F)!F)!F)!F
... There’s a very interesting property of cumulative distribution functions that is somewhat hard to believe. If { Fn } is any sequence of cumulative distribution functions, then there is a subsequence that converges to a cumulative (sub)distribution function F. The (sub) part of this comment is that t ...
... There’s a very interesting property of cumulative distribution functions that is somewhat hard to believe. If { Fn } is any sequence of cumulative distribution functions, then there is a subsequence that converges to a cumulative (sub)distribution function F. The (sub) part of this comment is that t ...
Exponential and Logarithmic Functions Honors Precalculus
... 1. The log of a number is the exponent when written in exponential form. 2. If the base of a logarithmic function is the irrational number e, then we have the natural logarithm function. This function is given a special symbol. That is y ln x iff x e y . 3. y ln x and x e y are inverse funct ...
... 1. The log of a number is the exponent when written in exponential form. 2. If the base of a logarithmic function is the irrational number e, then we have the natural logarithm function. This function is given a special symbol. That is y ln x iff x e y . 3. y ln x and x e y are inverse funct ...
1314Summer13.pdf
... The quantity denoted by the symbol e has special significance in mathematics. It is an irrational number that is the base of natural logarithms (to be discussed in the next lecture), and it is often seen in real world problems that involve natural exponential growth or decay. The approximated value ...
... The quantity denoted by the symbol e has special significance in mathematics. It is an irrational number that is the base of natural logarithms (to be discussed in the next lecture), and it is often seen in real world problems that involve natural exponential growth or decay. The approximated value ...
a 2
... This formula can also be rewritten in the following very useful form: P(a X b) F (b) F (a) ...
... This formula can also be rewritten in the following very useful form: P(a X b) F (b) F (a) ...
Slide 1
... Here, we study a new class of functions called exponential functions. For example, f(x) = 2x is an exponential function (with base 2). Notice how quickly the values of this function increase: f(3) = 23 = 8 f(10) = 210 = 1024 ...
... Here, we study a new class of functions called exponential functions. For example, f(x) = 2x is an exponential function (with base 2). Notice how quickly the values of this function increase: f(3) = 23 = 8 f(10) = 210 = 1024 ...
The Exponential Function A. Theorem 1 B. Example 1: Compound
... is e. Let En denote the nth term in this sequence. (For example, E1 = (1 + 1)1 , E2 = (1 + 1/2)2 , and in general Problem 5. Grains of wheat and chessboard En = (1 + 1/n)n .) (This problem was published by Ibn Kallikan in 1256. You can look it up on the Internet if you want to.) Calculate decimal va ...
... is e. Let En denote the nth term in this sequence. (For example, E1 = (1 + 1)1 , E2 = (1 + 1/2)2 , and in general Problem 5. Grains of wheat and chessboard En = (1 + 1/n)n .) (This problem was published by Ibn Kallikan in 1256. You can look it up on the Internet if you want to.) Calculate decimal va ...
Lecture13.pdf
... The quantity denoted by the symbol e has special significance in mathematics. It is an irrational number that is the base of natural logarithms, and it is often seen in real world problems that involve natural exponential growth or decay. The approximated value of e is 2.7182818284 . . . Students ca ...
... The quantity denoted by the symbol e has special significance in mathematics. It is an irrational number that is the base of natural logarithms, and it is often seen in real world problems that involve natural exponential growth or decay. The approximated value of e is 2.7182818284 . . . Students ca ...