symmetry-year-2-the-woods - Pembrokeshire Outdoor Schools
... Teacher to use a stick as a line of symmetry and pebbles, and make matching or non-matching patterns either side and ask group if they are symmetrical or not. Provide each child with a flattened circle of clay and ask them to mark out a line of symmetry (with a stick, leaves pebbles etc.). Onc ...
... Teacher to use a stick as a line of symmetry and pebbles, and make matching or non-matching patterns either side and ask group if they are symmetrical or not. Provide each child with a flattened circle of clay and ask them to mark out a line of symmetry (with a stick, leaves pebbles etc.). Onc ...
The challenge is to make an X-ray beam bright enough
... atoms in a crystal would interfere with one another to produce a pattern of light and dark spots or bands. This phenomenon is now called Bragg diffraction after the father-and-son team William and Lawrence Bragg. They showed in 1913 how these diffraction patterns could be mathematically decoded to f ...
... atoms in a crystal would interfere with one another to produce a pattern of light and dark spots or bands. This phenomenon is now called Bragg diffraction after the father-and-son team William and Lawrence Bragg. They showed in 1913 how these diffraction patterns could be mathematically decoded to f ...
M04CG1.1.3a Recognize a line of symmetry in a two
... Content Target: Given modeling and tangible 2 D shapes, students will select the shapes that demonstrates symmetry (parts that are the same size and shape) Example: Present students with concrete shapes of paper hearts (as examples.) Fold one heart along a line. Say when we folded object in two ...
... Content Target: Given modeling and tangible 2 D shapes, students will select the shapes that demonstrates symmetry (parts that are the same size and shape) Example: Present students with concrete shapes of paper hearts (as examples.) Fold one heart along a line. Say when we folded object in two ...
M04CG1.1.3a Recognize a line of symmetry in a two
... • Content Target: Given modeling and tangible 2 D shapes, students will select the shapes that demonstrates symmetry (parts that are the same size and shape) • Example: Present students with concrete shapes of paper hearts (as examples.) Fold one heart along a line. Say when we folded object in two ...
... • Content Target: Given modeling and tangible 2 D shapes, students will select the shapes that demonstrates symmetry (parts that are the same size and shape) • Example: Present students with concrete shapes of paper hearts (as examples.) Fold one heart along a line. Say when we folded object in two ...
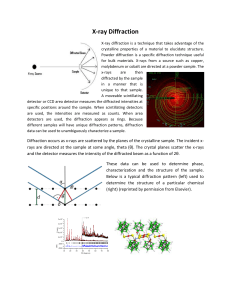
X-ray Diffraction
... generated. Anodes are often made of copper, iron or molybdenum. 2- X-rays are electromagnetic radiation. 3- They have enough energy to cause ionization. ...
... generated. Anodes are often made of copper, iron or molybdenum. 2- X-rays are electromagnetic radiation. 3- They have enough energy to cause ionization. ...
2D and 3D Design Notes
... b) Using Symmetry and Some Trig to Construct the Rhombicuboctahedron and the Rhombi Truncated Cuboctahedron c) Using Truncation to Construct The Truncated Icosahedron, The Truncated Dodecahedron and The Icosadocecahedron e) Using Symmetry and Some Trig to Construct the Rhombicosadodecahedron and the ...
... b) Using Symmetry and Some Trig to Construct the Rhombicuboctahedron and the Rhombi Truncated Cuboctahedron c) Using Truncation to Construct The Truncated Icosahedron, The Truncated Dodecahedron and The Icosadocecahedron e) Using Symmetry and Some Trig to Construct the Rhombicosadodecahedron and the ...
Small molecule Crystallography at the Indian Institute of Science
... backbone modifications has provided a systematic base for understanding of heterogeneity and stability of helices, helical transition, reversal, termination, hydration and solvation of helices, unfolding of helices, helix orientation and mode of assembly of helices in peptide crystals. While in the ...
... backbone modifications has provided a systematic base for understanding of heterogeneity and stability of helices, helical transition, reversal, termination, hydration and solvation of helices, unfolding of helices, helix orientation and mode of assembly of helices in peptide crystals. While in the ...
X‐ray diffraction: Determining lattice constants of crystal structure
... 3) Look up the lattice constants for your two samples and make a table of the expected diffraction angles for the first 3 orders for the Kα and Kβ x-ray peaks for each sample using Equation (3). These should be written up separately and handed in at the laboratory session when the experiment is ...
... 3) Look up the lattice constants for your two samples and make a table of the expected diffraction angles for the first 3 orders for the Kα and Kβ x-ray peaks for each sample using Equation (3). These should be written up separately and handed in at the laboratory session when the experiment is ...
X-ray Diffraction
... Single crystal diffraction is another type of diffraction which uses large single crystals to obtain diffraction data. Diffraction occurs exactly the same way as it does in powders, but because single crystals are used, the orientation of the crystal must always be known. In addition, area CCD area ...
... Single crystal diffraction is another type of diffraction which uses large single crystals to obtain diffraction data. Diffraction occurs exactly the same way as it does in powders, but because single crystals are used, the orientation of the crystal must always be known. In addition, area CCD area ...
Diffraction maxima include diffraction from All atoms in the crystal
... Fhkl = V∑∑∑ρxyz cos [2π(hx+ky+lz)] + ρxyz sin [2π(hx+ky+lz)] ...
... Fhkl = V∑∑∑ρxyz cos [2π(hx+ky+lz)] + ρxyz sin [2π(hx+ky+lz)] ...
Why do scientists grow crystals? - Bryn Mawr School Faculty Web
... Substances grown in crystals are extremely pure. These are insulin crystals, grown to purify the insulin used by diabetics ...
... Substances grown in crystals are extremely pure. These are insulin crystals, grown to purify the insulin used by diabetics ...
syllabus
... Description and rationale: The aim of this course is to provide basic knowledge of diffraction from condensed matter (sold, liquid and gas). The main focus will be on X-ray diffraction and neutron scattering from crystals. This course will provide the attendee with the following essential understand ...
... Description and rationale: The aim of this course is to provide basic knowledge of diffraction from condensed matter (sold, liquid and gas). The main focus will be on X-ray diffraction and neutron scattering from crystals. This course will provide the attendee with the following essential understand ...
0378.PDF
... a energetically more favorable hydrodynamically compressed state by slippage or phase transformations. Often stacking faults are created which permit a simple detection of slippage. For a crystal it is rather easy to construct slip planes and stacking faults and to analyze them. This is not the case ...
... a energetically more favorable hydrodynamically compressed state by slippage or phase transformations. Often stacking faults are created which permit a simple detection of slippage. For a crystal it is rather easy to construct slip planes and stacking faults and to analyze them. This is not the case ...
Quasicrystal

A quasiperiodic crystal, or quasicrystal, is a structure that is ordered but not periodic. A quasicrystalline pattern can continuously fill all available space, but it lacks translational symmetry. While crystals, according to the classical crystallographic restriction theorem, can possess only two, three, four, and six-fold rotational symmetries, the Bragg diffraction pattern of quasicrystals shows sharp peaks with other symmetry orders, for instance five-fold.Aperiodic tilings were discovered by mathematicians in the early 1960s, and, some twenty years later, they were found to apply to the study of quasicrystals. The discovery of these aperiodic forms in nature has produced a paradigm shift in the fields of crystallography. Quasicrystals had been investigated and observed earlier, but, until the 1980s, they were disregarded in favor of the prevailing views about the atomic structure of matter. In 2009, after a dedicated search, a mineralogical finding, icosahedrite, offered evidence for the existence of natural quasicrystals.Roughly, an ordering is non-periodic if it lacks translational symmetry, which means that a shifted copy will never match exactly with its original. The more precise mathematical definition is that there is never translational symmetry in more than n – 1 linearly independent directions, where n is the dimension of the space filled, e.g., the three-dimensional tiling displayed in a quasicrystal may have translational symmetry in two dimensions. The ability to diffract comes from the existence of an indefinitely large number of elements with a regular spacing, a property loosely described as long-range order. Experimentally, the aperiodicity is revealed in the unusual symmetry of the diffraction pattern, that is, symmetry of orders other than two, three, four, or six. In 1982 materials scientist Dan Shechtman observed that certain aluminium-manganese alloys produced the unusual diffractograms which today are seen as revelatory of quasicrystal structures. Due to fear of the scientific community's reaction, it took him two years to publish the results for which he was awarded the Nobel Prize in Chemistry in 2011.